
【题目】今年我省部分地区遭遇严重干旱,为鼓励市民节约用水,我市自来水公司按分段收费标准收费,右图反映的是每月收水费y(元)与用水量x(吨)之间的函数关系.
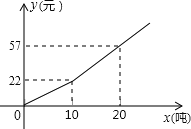
(1)小聪家五月份用水7吨,应交水费 元;
(2)按上述分段收费标准,小聪家三、四月份分别交水费29元和19.8元,问四月份比三月份节约用水多少吨?
【答案】(1)15.4;(2)3吨.
【解析】
(1)从函数图象可知10吨水以内的价格是每吨2.2元,小聪家五月份用水7吨,应交水费可计算得到;
(2)先设函数解析式,然后看图将对应值代入其中求出常数项,即可得到函数解析式,根据函数解析式求出四月份的水量,三月份水量可直接求,那么四月份比三月份节约用水多少可求出.
(1)从函数图象可知10吨水应交22元,
那么每吨水的价格是:22÷10=2.2(元)
小聪家五月份用水7吨,应交水费:
7×2.2=15.4(元)
答:应交水费15.4元;
(2)由图可得10吨内每吨2.2元,当y=19.8元时,x<10,
∴x=19.8÷2.2=9,
当x≥10时,设y与x的函数关系式为:y=kx+b(k≠0),
当x=10时,y=22,当x=20时,y=57,
将它们分别代入y=kx+b中得:
![]() 解得
解得![]() ,
,
那么y与x的函数关系式为:y=3.5x-13,
当y=29时,知道x>10,将y=29代入得
y=3.5x-13,
解得x=12.
四月份比三月份节约用水:12-9=3(吨).


科目:初中数学 来源: 题型:
【题目】如图是某货站传送货物的平面示意图为了提高传送过程的安全性,工人师傅欲减小传送带与地面的夹角使其由![]() 改为
改为![]() ,已知原传送带
,已知原传送带![]() 长为4米.
长为4米.
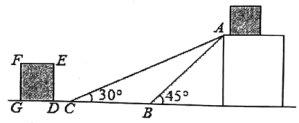
(1)求新传送带![]() 的长度;(结果保留根号)
的长度;(结果保留根号)
(2)如果需要在货物着地点![]() 的左侧留出2米的通道,试判断距离
的左侧留出2米的通道,试判断距离![]() 点5米的货物
点5米的货物![]() 是否需要挪走,并说明理由(结果精确到0.1米参考数据:
是否需要挪走,并说明理由(结果精确到0.1米参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直线m上摆放着三个正三角形:△ABC,△HFG,△DCE,已知BC=![]() CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1、S2、S3,若S1+S3=10,则S2=___________.
CE,F、G分别是BC、CE的中点,FM∥AC,GN∥DC.设图中三个平行四边形的面积依次是S1、S2、S3,若S1+S3=10,则S2=___________.
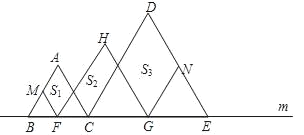
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线![]() 与
与![]() 轴相交于点
轴相交于点![]() ,与
,与![]() 轴相交于
轴相交于![]() ,抛物线
,抛物线![]() 经过两点
经过两点![]() ,与
,与![]() 轴另一交点为
轴另一交点为![]() .
.
(1)求抛物线的解析式;
(2)如图1,过点![]() 作
作![]() 轴,交抛物线于另一点
轴,交抛物线于另一点![]() ,点
,点![]() 以每秒
以每秒![]() 个单位长度的速度在线段
个单位长度的速度在线段![]() 上由点
上由点![]() 向点
向点![]() 运动(点
运动(点![]() 不与点
不与点![]() 和点
和点![]() 重合),设运动时间为
重合),设运动时间为![]() 秒,过点
秒,过点![]() 作
作![]() 轴交
轴交![]() 于点
于点![]() ,作
,作![]() 于点
于点![]() ,交
,交![]() 轴右侧的抛物线与点
轴右侧的抛物线与点![]() ,连接
,连接![]() ,当
,当![]() 时,求
时,求![]() 的值;
的值;
(3)如图2,正方形![]() ,边
,边![]() 在
在![]() 轴上,点
轴上,点![]() 与点
与点![]() 重合,边长
重合,边长![]() 为
为![]() 个单位长度,将正方形
个单位长度,将正方形![]() 沿射线
沿射线![]() 方向,以每秒
方向,以每秒![]() 个单位长度的速度平移,时间为
个单位长度的速度平移,时间为![]() 秒,在平移过程中,请写出正方形
秒,在平移过程中,请写出正方形![]() 的边恰好与抛物线有两个交点时
的边恰好与抛物线有两个交点时![]() 的取值范围.
的取值范围.
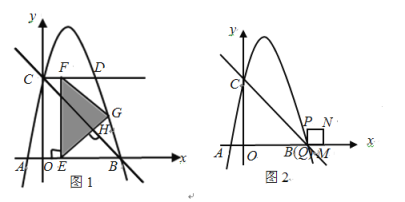
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2+bx+c(a<0)与x轴交于点A(﹣1,0),与y轴的交点在(0,2),(0,3)之间(包含端点),顶点坐标为(1,n),则下列结论:
①4a+2b<0;
②﹣1≤a≤![]() ;
;
③对于任意实数m,a+b≥am2+bm总成立;
④关于x的方程ax2+bx+c=n﹣1有两个不相等的实数根.
其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴相交于
轴相交于![]() ,
,![]() 两点,与
两点,与![]() 轴相交于点
轴相交于点![]() ,顶点为
,顶点为![]() ,直线
,直线![]() 与
与![]() 轴相交于点
轴相交于点![]()
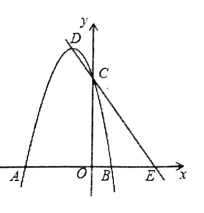
(1)求抛物线的顶点坐标(用含![]() 的式子表示);
的式子表示);
(2)![]() 的长是否与
的长是否与![]() 值有关,说明你的理由;
值有关,说明你的理由;
(3)设![]() ,求
,求![]() 的取值范围;
的取值范围;
(4)以![]() 为斜边,在直线
为斜边,在直线![]() 的左下方作等腰直角三角形
的左下方作等腰直角三角形![]() .设
.设![]() ,直接写出
,直接写出![]() 关于
关于![]() 的函数解析式及自变量
的函数解析式及自变量![]() 的取值范围.
的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,AB=6,AD=9,∠BAD的平分线交BC于点E,交DC的延长线于点F,BG⊥AE,垂足为G,若BG=![]() ,则△CEF的面积是( )
,则△CEF的面积是( )
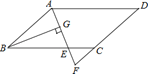
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
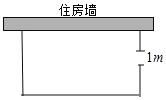
【题目】如图,一农户要建一个矩形猪舍,猪舍的一边利用长为15m的住房墙,另外三边用27m长的建筑材料围成,为方便进出,在垂直于住房墙的一边留一个1m宽的门,所围矩形猪舍的长,宽分别为多少米时,猪舍面积为96m2?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com