
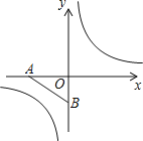
【题目】在平面直角坐标系中,已知点A、B的坐标分别为(-![]() ,0)、(0,-1),把点A绕坐标原点O顺时针旋转135°得点C,若点C在反比例函数y=
,0)、(0,-1),把点A绕坐标原点O顺时针旋转135°得点C,若点C在反比例函数y=![]() 的图象上.
的图象上.
(1)求反比例函数的表达式;
(2)若点D在y轴上,点E在反比例函数y=![]() 的图象上,且以点A、B、D、E为顶点的四边形是平行四边形.请画出满足题意的示意图并在示意图的下方直接写出相应的点D、E的坐标.
的图象上,且以点A、B、D、E为顶点的四边形是平行四边形.请画出满足题意的示意图并在示意图的下方直接写出相应的点D、E的坐标.
【答案】(1)y=![]() ;(2)示意图见解析,E(-
;(2)示意图见解析,E(-![]() ,-
,-![]() ),D(0,-1-
),D(0,-1-![]() )或E(-
)或E(-![]() ,-
,-![]() ),D(0,-1+
),D(0,-1+![]() )或E
)或E 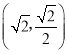 , D
, D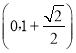
【解析】
(1)根据旋转和直角三角形的边角关系可以求出点C的坐标,进而确定反比例函数的关系式;
(2)分两种情况进行讨论解答,①点E在第三象限,由题意可得E的横坐标与点A的相同,将A的横坐标代入反比例函数的关系式,可求出纵坐标,得到E的坐标,进而得到AE的长,也是BD的长,因此D在B的上方和下方,即可求出点D的坐标,②点E在第一象限,由三角形全等,得到E的横坐标,代入求出纵坐标,确定E的坐标,进而求出点D的坐标.
(1)由旋转得:OC=OA=![]() ,∠AOC=135°,
,∠AOC=135°,
过点C作CM⊥y轴,垂足为M,则∠COM=135°-90°=45°,
在Rt△OMC中,∠COM=45°,OC=![]() ,
,
∴OM=CM=1,
∴点C(1,1),代入y=![]() 得:k=1,
得:k=1,
∴反比例函数的关系式为:y=![]() ,
,
答:反比例函数的关系式为:y=![]()
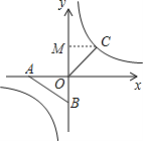
(2)①当点E在第三象限反比例函数的图象上,如图1,图2,
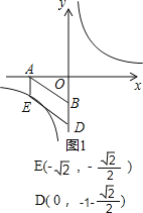
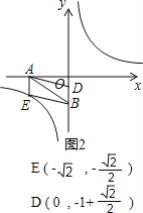
∵点D在y轴上,AEDB是平行四边形,
∴AE∥DB,AE=BD,AE⊥OA,
当x=-![]() 时,y=
时,y=![]() =-
=-![]() ,
,
∴E(-![]() ,-
,-![]() )
)
∵B(0,-1),BD=AE=![]() ,
,
当点D在B的下方时,
∴D(0,-1-![]() )
)
当点D在B的上方时,
∴D(0,-1+![]() ),
),
②当点E在第一象限反比例函数的图象上时,如图3,
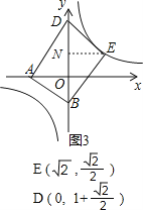
过点E作EN⊥y轴,垂足为N,
∵ABED是平行四边形,
∴AB=DE,AB=DE,
∴∠ABO=∠EDO,
∴△AOB≌△END (AAS),
∴EN=OA=![]() ,DN=OB=1,
,DN=OB=1,
当x=![]() 时,代入y=
时,代入y=![]() 得:y=
得:y=![]() ,
,
∴E(![]() ,
,![]() ),
),
∴ON=![]() ,OD=ON+DN=1+
,OD=ON+DN=1+![]() ,
,
∴D(0,1+![]() )
)


 小学教材完全解读系列答案
小学教材完全解读系列答案科目:初中数学 来源: 题型:
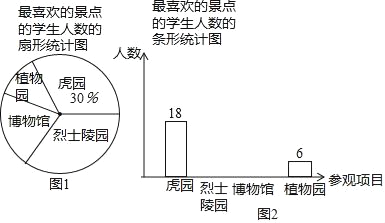
【题目】某校在一次社会实践活动中,组织学生参观了虎园、烈士陵园、博物馆和植物园,为了解本次社会实践活动的效果,学校随机抽取了部分学生,对“最喜欢的景点”进行了问卷调查,并根据统计结果绘制了如下不完整的统计图.其中最喜欢烈士陵园的学生人数与最喜欢博物馆的学生人数之比为2:1,请结合统计图解答下列问题:
(1)本次活动抽查了 名学生;
(2)请补全条形统计图;
(3)在扇形统计图中,最喜欢植物园的学生人数所对应扇形的圆心角是 度;
(4)该校此次参加社会实践活动的学生有720人,请求出最喜欢烈士陵园的人数约有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
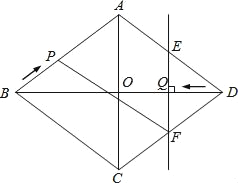
【题目】如图,在菱形ABCD中,AC,BD交于点O,且AC=12cm,BD=16cm.点P从点B出发,沿BA方向匀速运动,速度为lcm/s;同时,直线EF从点D出发,沿DB方向匀速运动,速度为lcm/s,EF⊥BD,且与AD,BD,CD分别交于点E,Q.F,当直线EF停止运动时,点P也停止运动.连接PF,设运动时间为t(s)(0<t<8).解答下列问题:
(1)求菱形ABCD的面积;
(2)当t=1时,求QF长;
(3)是否存在某一时刻t,使四边形APFD是平行四边形?若存在,求出t值,若不存在,请说明理由;
(4)设△DEF的面积为s(cm2),试用含t的代数式表示S,并求t为何值时,△DEF的面积与△BPC的面积相等.
查看答案和解析>>
科目:初中数学 来源: 题型:
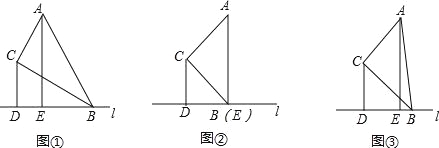
【题目】在△ABC中,∠ACB=90°经过点B的直线l(l不与直线AB重合)与直线BC的夹角等于∠ABC,分别过点C、A做直线l的垂线,垂足分别为点D、E.
(1)问题发现:
①若∠ABC=30°,如图①,则![]() = ;
= ;
②∠ABC=45°,如图②,则![]() = ;
= ;
(2)拓展探究:
当0°<∠ABC<90°,![]() 的值有无变化?请仅就图③的情形给出证明.
的值有无变化?请仅就图③的情形给出证明.
(3)问题解决:
若直线CE、AB交于点F,![]() =
=![]() ,CD=4,请直接写出线段BD的长.
,CD=4,请直接写出线段BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某工厂将地处A,B两地的两个小工厂合成一个大厂,为了方便A,B两地职工的联系,企业准备在相距2km的A,B两地之间修一条笔直的公路(即图中的线段AB),经测量在A地的北偏东60°方向,B地的北偏西45°方向的C处有一以C点为中心,半径为0.7km的圆形公园,则修筑的这条公路会不会穿过公园?为什么?(提示:判断以点C为圆心的圆与AB的关系)
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
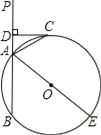
【题目】如图,已知直线PA交⊙O于A、B两点,AE是⊙O的直径,点C为⊙O上一点,且AC平分∠PAE,过C作CD⊥PA,垂足为D.
(1)求证:CD为⊙O的切线;
(2)若DC+DA=6,⊙O的直径为10,求AB的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋中装有4张卡片,卡片上分別标有数字1、﹣2、3、﹣4,这些卡片除数字外都相同.王兴从口袋中随机抽取一张卡片,钟华从剩余的三张卡片中随机抽取一张,求两张卡片上数字之积.
(1)请你用画树状图或列表的方法,列出两人抽到的数字之积所有可能的结果.
(2)求两人抽到的数字之积为正数的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场进行促销,购物满额即可获得1次抽奖机会,抽奖袋中装有红色、黄色、白色三种除颜色外都相同的小球,从袋子中摸出1个球,红色、黄色、白色分别代表一、二、三等奖.
(1)若小明获得1次抽奖机会,小明中奖是 事件;(填随机、必然、不可能)
(2)小明观察一段时间后发现,平均每8个人中会有1人抽中一等奖,2人抽中二等奖,若袋中共有24个球,请你估算袋中白球的数量;
(3)在(2)的条件下,如果在抽奖袋中减少3个白球,那么抽奖一次恰好抽中一等奖的概率是多少?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com