
【题目】如图,∠AOB=30°,点M,N分别在边OA,OB上,OM=5,ON=12,点P,Q分别在边OB,OA上运动,连接MP,PQ,QN,则MP+PQ+QN的最小值为 ______ .

科目:初中数学 来源: 题型:
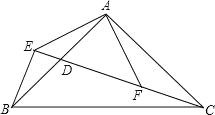
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.
(1)求证:AE=AF;
(2)求证:CD=2BE+DE.
查看答案和解析>>
科目:初中数学 来源: 题型:
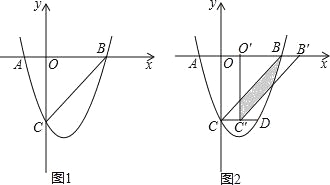
【题目】如图,抛物线y=ax2+bx+c(a≠0)与x轴、y轴分别交于点A(﹣1,0),B(3,0)、C(0,﹣3)三点.
(1)直接写出抛物线的解析式 ;
(2)点D(2,m)在第一象限的抛物线上,连接BC、BD,试问,在对称轴左侧的抛物线上是否存在一点P,满足∠PBC=∠DBC?如果存在,请求出点P点的坐标;如果不存在,请说明理由.
(3)如图2,在(2)的条件下,将△BOC沿x轴正方向以每秒1个单位长度的速度向右平移,记平移后的三角形为△B′O′C′,在平移过程中,△B′O′C′与△BCD重叠的面积记为S,设平移的时间为t秒(0≤t≤3),试求S与t之间的函数关系式?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法中,其中正确的个数是( )
(1)有理数中,有绝对值最小的数;(2)有理数不是整数就是分数;(3)当a表示正有理数,则-a一定是负数;(4)a是大于-1的负数,则a2小于a3
A. 1 B. 2 C. 3 D. 4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列条件中不能判定△ABM≌△CDN的是( )

A. ∠M=∠N B. AM=CN C. AB=CD D. AM∥CN
查看答案和解析>>
科目:初中数学 来源: 题型:
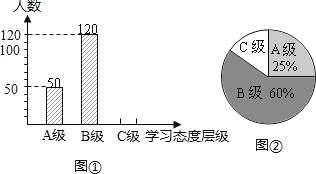
【题目】某地教育部门对九年级学生的“学习态度”进行了一次抽样调查,把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣,要求被调查的学生从A、B、C三项中必选且只能选择一项,结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
(1)此次抽样调查中,共调查了 名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计该地8000名九年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com