
【题目】如图,在△ABC中,∠BAC=90°,AB=AC,点D是AB的中点,连接CD,过B作BE⊥CD交CD的延长线于点E,连接AE,过A作AF⊥AE交CD于点F.
(1)求证:AE=AF;
(2)求证:CD=2BE+DE.
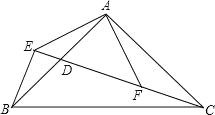
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、通过证△AEB≌△AFC(SAS),得到AE=AF;(2)、如图,过点A作AG⊥EC,垂足为G,通过证△BED≌△AGD(AAS),得到ED=GD,BE=AG,易证CF=BE=AG=GF.因为CD=DG+GF+FC,所以CD=DE+BE+BE,故CD=2BE+DE.
试题解析:(1)、如图,∵∠BAC=90°,AF⊥AE, ∴∠EAB+∠BAF=∠BAF+∠FAC=90°,
∴∠EAB=∠FAC, ∵BE⊥CD, ∴∠BEC=90°, ∴∠EBD+∠EDB=∠ADC+∠ACD=90°,
∵∠EDB=∠ADC, ∴∠EBA=∠ACF, ∴在△AEB与△AFC中,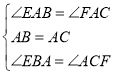 ,
,
∴△AEB≌△AFC(ASA), ∴AE=AF;
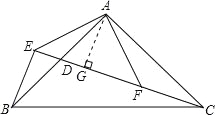
(2)、如图,过点A作AG⊥EC,垂足为G. ∵AG⊥EC,BE⊥CE, ∴∠BED=∠AGD=90°,
∵点D是AB的中点, ∴BD=AD. ∴在△BED与△AGD中,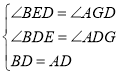 , ∴△BED≌△AGD(AAS), ∴ED=GD,BE=AG, ∵AE=AF ∴∠AEF=∠AFE=45° ∴∠FAG=45° ∴∠GAF=∠GFA, ∴GA=GF, ∴CF=BE=AG=GF, ∵CD=DG+GF+FC, ∴CD=DE+BE+BE, ∴CD=2BE+DE.
, ∴△BED≌△AGD(AAS), ∴ED=GD,BE=AG, ∵AE=AF ∴∠AEF=∠AFE=45° ∴∠FAG=45° ∴∠GAF=∠GFA, ∴GA=GF, ∴CF=BE=AG=GF, ∵CD=DG+GF+FC, ∴CD=DE+BE+BE, ∴CD=2BE+DE.


科目:初中数学 来源: 题型:
【题目】微电子技术的不断进步,使半导体材料的精细加工尺寸大幅度缩小.某种电子元件的面积大约为0.000000 7平方毫米,用科学记数法表示为平方毫米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城街路上行驶速度不得超过70km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪A处的正前方30m的C处,过了2s后,测得小汽车与车速检测仪间距离为50m,这辆小汽车超速了吗?(参考数据转换:1m/s=3.6km/h)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线与x轴交于A(6,0)、B(![]() ,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
,0)两点,与y轴交于点C,过抛物线上点M(1,3)作MN⊥x轴于点N,连接OM.
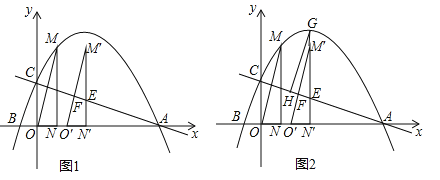
(1)求此抛物线的解析式;
(2)如图1,将△OMN沿x轴向右平移t个单位(0≤t≤5)到△O′M′N′的位置,MN′、M′O′与直线AC分别交于点E、F.
①当点F为M′O′的中点时,求t的值;
②如图2,若直线M′N′与抛物线相交于点G,过点G作GH∥M′O′交AC于点H,试确定线段EH是否存在最大值?若存在,求出它的最大值及此时t的值;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
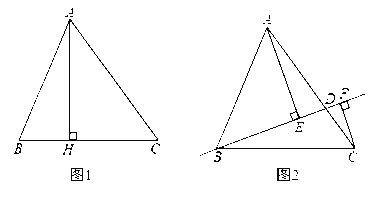
【题目】如图1和2,在△ABC中,AB=13,BC=14,BH=5.
探究:如图1,AH⊥BC于点H,则AH= ,AC= ,△ABC的面积![]() ;
;
拓展:如图2,点D在AC上(可与点A,C重合),分别过点A.C作直线BD的垂线,垂足为E,F,设BD=x,AE=m,CF=n(当点D与点A重合时,我们认为![]() )
)
(1)用含x,m,n的代数式表示![]() 及
及![]() ;
;
(2)求(m+n)与x的函数关系式,并求(m+n)的最大值和最小值;
(3)对给定的一个x值,有时只能确定唯一的点D,直接写出这样的x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为a的正方形中挖去一个边长为b的小正方形(a>b)(如图甲),把余下的部分拼成一个矩形(如图乙),根据两个图形中阴影部分的面积相等,可以验证( )

A. (a+b)2=a2+2ab+b2 B. (a﹣b)2=a2-2ab+b2
C. (a+b)(a﹣b)= a2﹣b2 D. (a+2b)(a﹣b)=a2+ab﹣2b2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com