
【题目】二次函数y=ax2+bx+c的自变量x与函数值y的部分对应值如下表:
x | … | ﹣1 | 0 | 1 | 2 | 3 | … |
y | … | ﹣1 | ﹣ | ﹣2 | ﹣ | … |
根据表格中的信息,完成下列各题
(1)当x=3时,y=
(2)当x为何值时,y=0?
(3)①若自变量x的取值范围是0≤x≤5,求函数值y的取值范围;
②若函数值y为正数,则自变量x的取值范围.
【答案】(1)-1(2)1±2![]() (3)①﹣2≤x≤2②x<1﹣2
(3)①﹣2≤x≤2②x<1﹣2![]() 或x>1+2
或x>1+2![]()
【解析】
(1)从表格看出,函数的对称轴为x=1,顶点为(1,﹣2),x=3和x=﹣1时关于对称轴的对称点,故x=3时,y=﹣1;
(2)把顶点坐标、点(﹣1,﹣1)代入函数表达式,即可求解;
(3)①当0≤x≤5,函数在顶点处取得最小值,在x=5时,函数取得最大值,即可求解;②若函数值y为正数,则x<1﹣2![]() 或x>1+2
或x>1+2![]() .
.
(1)从表格看出,函数的对称轴为x=1,顶点为(1,﹣2),故x=3时,y=﹣1,
故:答案是﹣1;
(2)把顶点坐标代入二次函数顶点式表达式得:y=a(x﹣1)2﹣2,
把点(﹣1,﹣1)代入上式得:﹣1=a(﹣1﹣1)2﹣2,解得:a=![]() ,
,
则函数表达式为:y=![]() (x﹣1)2﹣2,
(x﹣1)2﹣2,
令y=0,则x=1±2![]() ;
;
(3)①当0≤x≤5,函数在顶点处取得最小值,y=﹣2,
当x=5时,函数取得最大值y=![]() (5﹣1)2﹣2=2,
(5﹣1)2﹣2=2,
即:函数值y的取值范围为:﹣2≤x≤2;
②若函数值y为正数,则x<1﹣2![]() 或x>1+2
或x>1+2![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC=10,点D是边BC上一动点 (不与B,C重合),∠ADE=∠B=α,DE交AC于点E,且 ![]() .下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或
.下列结论: ①△ADE∽△ACD;②当BD=6时,△ABD与△DCE全等;③△DCE为直角三角形时,BD为8或![]() ;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)
;④CD2=CECA.其中正确的结论是________(把你认为正确结论的序号都填上)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,∠BAD=80°,AB的垂直平分线交对角线AC于点F,E为垂足,连结DF,则∠CDF等于( )

A. 80° B. 70° C. 65° D. 60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在南北方向的海岸线MN上,有A、B两艘巡逻船,现均收到故障船C的求救信号.已知A、B两船相距100(![]() +1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
+1)海里,船C在船A的北偏东60°方向上,船C在船B的东南方向上,MN上有一观测点D,测得船C正好在观测点D的南偏东75°方向上.
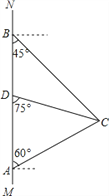
(1)分别求出A与C,A与D间的距离AC和AD(如果运算结果有根号,请保留根号).
(2)已知距离观测点D处100海里范围内有暗礁,若巡逻船A沿直线AC去营救船C,在去营救的途中有无触礁的危险?(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73)
≈1.73)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示是一个几何体的三视图.
(1)写出这个几何体的名称;
(2)根据图中数据计算这个几何体的表面积;
(3)如果一只蚂蚁要从这个几何体上的点B出发,沿表面爬到AC的中点D,请你求出这条路线的最短路程.
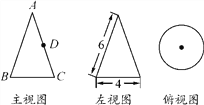
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知△ABC是等边三角形.
(1)将△ABC绕点A逆时针旋转角θ(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O.
①如图a,当θ=20°时,△ABD与△ACE是否全等? (填“是”或“否”),∠BOE= 度;
②当△ABC旋转到如图b所在位置时,求∠BOE的度数;
(2)如图c,在AB和AC上分别截取点B′和C′,使AB=![]() AB′,AC=
AB′,AC=![]() AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.
AC′,连接B′C′,将△AB′C′绕点A逆时针旋转角(0°<θ<180°),得到△ADE,BD和EC所在直线相交于点O,请利用图c探索∠BOE的度数,直接写出结果,不必说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,把平面内一条数轴x绕原点O逆时针旋转角θ(0°<θ<90°)得到另一条数轴y,x轴和y轴构成一个平面斜坐标系.规定:过点P作y轴的平行线,交x轴于点A,过点P作x轴的平行线,交y轴于点B,若点A在x轴上对应的实数为a,点B在y轴上对应的实数为b,则称有序实数对(a,b)为点P的斜坐标,在某平面斜坐标系中,已知θ=60°,点M′的斜坐标为(3,2),点N与点M关于y轴对称,则点N的斜坐标为_____.
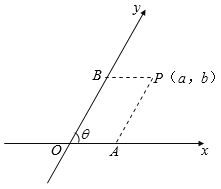
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,AC为弦,∠BAC的平分线交⊙O于点D,过点D的切线交AC的延长线于点E.
求证:(1)DE⊥AE;
(2)AE+CE=AB.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com