
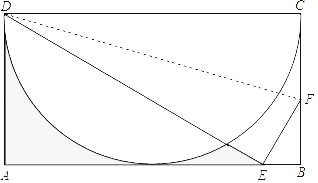
【题目】如图所示,ABCD为矩形,以CD为直径作半圆,矩形的另外三边分别与半圆相切,沿着折痕DF折叠该矩形,使得点C的对应点E落在AB边上,若AD=2,则图中阴影部分的面积为_____.
【答案】![]()
【解析】
作OH⊥AB于H,DE交半圆于M,连接OM,作ON⊥DM于N,如图,利用切线的性质得CD=2OH=4,再根据折叠的性质得DE=DC=4,则根据正弦的定义得到∠AED=30°,AE=![]() ,AD=2
,AD=2![]() ,接着求出∠DOM=120°,然后根据三角形面积公式、扇形的面积公式,利用图中阴影部分的面积=S△ADE﹣S弓形DHM=S△ADE﹣(S扇形DOM﹣S△DOM)进行计算.
,接着求出∠DOM=120°,然后根据三角形面积公式、扇形的面积公式,利用图中阴影部分的面积=S△ADE﹣S弓形DHM=S△ADE﹣(S扇形DOM﹣S△DOM)进行计算.
解:作OH⊥AB于H,DE交半圆于M,连接OM,作ON⊥DM于N,如图,
∵矩形的另外三边分别与半圆相切,
∴OH为半圆的半径,
∴CD=2OH=2AD=4,
∵DC沿DF折叠到DE,
∴DE=DC=4,
在Rt△ADE中,∵sin∠AED=![]() ,
,
∴∠AED=30°,
∴AE=![]() ,AD=2
,AD=2![]() ,
,
∵CD∥AB,
∴∠CDE=∠AEB=30°,
∵OD=OM,
∴∠ODM=∠OMD=30°,
∴∠DOM=120°,
∴图中阴影部分的面积=S△ADE﹣S弓形DHM=S△ADE﹣(S扇形DOM﹣S△DOM)=![]() .
.
故答案为![]() .
.


科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立一个可自由转动的转盘,(如图,3个数字所在的扇形面积相等)并规定,顾客每购满100元商品,可转动两次转盘,转盘停止后,看指针指向的数.(如果指针指向分界线,则重新转动转盘,直到指针指向数为止)获奖方法是:①指针两次都指向3,顾客可获得90元购物券,②指针只有一次指向3,顾客可得36元购物券,③指针两次都不指向3,顾客只能获得18元购物券;若顾客不愿转动转盘,则可直接获得30元购物券
(1)试用树状图或列表法给出两次转动转盘指针所有可能指向的结果;
(2)请分别求顾客获得90元,36元,18元购物券的概率;
(3)你认为转动转盘和直接获得购物券哪种方式更合算?试说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
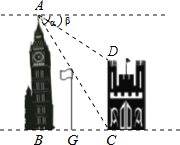
【题目】如图,在两建筑物之间有一旗杆,高15米,从A点经过旗杆顶点恰好看到矮建筑物的墙角C点,且俯角α为60°,又从A点测得D点的俯角β为30°,若旗杆底部G点为BC的中点,求矮建筑物的高CD.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 与x轴交于点A、B(点A位于点B左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
与x轴交于点A、B(点A位于点B左侧),与y轴交于点C,CD∥x轴交抛物线于点D,M为抛物线的顶点.
(1)求点A、B、C的坐标;
(2)设动点N(-2,n),求使MN+BN的值最小时n的值;
(3)P是抛物线上位于x轴上方的一点,请探究:是否存在点P,使以P、A、B为顶点的三角形与△ABD相似?若存在,求出点P的坐标;若不存在,请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知A(3,m),B(﹣2,﹣3)是直线AB和某反比例函数的图象的两个交点.
(1)求直线AB和反比例函数的解析式;
(2)观察图象,直接写出当x满足什么范围时,直线AB在双曲线的下方;
(3)反比例函数的图象上是否存在点C,使得△OBC的面积等于△OAB的面积?如果不存在,说明理由;如果存在,求出满足条件的所有点C的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,AB=8,点P在边CD上,tan∠PBC=![]() ,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
,点Q是在射线BP上的一个动点,过点Q作AB的平行线交射线AD于点M,点R在射线AD上,使RQ始终与直线BP垂直.
(1)如图1,当点R与点D重合时,求PQ的长;
(2)如图2,试探索: ![]() 的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
的比值是否随点Q的运动而发生变化?若有变化,请说明你的理由;若没有变化,请求出它的比值;
(3)如图3,若点Q在线段BP上,设PQ=x,RM=y,求y关于x的函数关系式,并写出它的定义域.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣x2+3x+4交x轴于A、B两点(点A在B左边),交y轴于点C.
(1)求A、B两点的坐标;
(2)求直线BC的函数关系式;
(3)点P在抛物线的对称轴上,连接PB,PC,若△PBC的面积为4,求点P的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
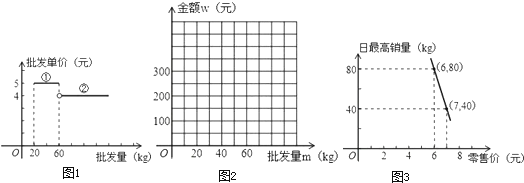
【题目】已知某种水果的批发单价与批发量的函数关系如图1所示.
(1)请说明图中①、②两段函数图象的实际意义;
(2)写出批发该种水果的资金金额w(元)与批发量m(kg)之间的函数关系式;在图2的坐标系中画出该函数图象;指出金额在什么范围内,以同样的资金可以批发到较多数量的该种水果;
(3)经调查,某经销商销售该种水果的日最高销量与零售价之间的函数关系如图3所示,该经销商拟每日售出60kg以上该种水果,且当日零售价不变,请你帮助该经销商设计进货和销售的方案,使得当日获得的利润最大.
查看答案和解析>>
科目:初中数学 来源: 题型:
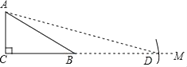
【题目】如何求tan75°的值?按下列方法作图可解决问题,如图,在Rt△ABC中,AC=k,∠ACB=90°,∠ABC=30°,延长CB至点M,在射线BM上截取线段BD,使BD=AB,连接AD,依据此图可求得tan75°的值为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com