
����Ŀ���Ķ����в��ϣ�
����֪��![]() �ļ�������������������
�ļ�������������������![]() ��Ӧ�ĵ���ԭ��ľ��룬��
��Ӧ�ĵ���ԭ��ľ��룬��![]() ��Ҳ����˵��
��Ҳ����˵��![]() ��ʾ����������
��ʾ����������![]() ����
����![]() ��Ӧ�ĵ�֮��ľ��룻
��Ӧ�ĵ�֮��ľ��룻
�� 1���ⷽ��![]() ����Ϊ�������ϵ�ԭ��ľ���Ϊ
����Ϊ�������ϵ�ԭ��ľ���Ϊ![]() �ĵ��Ӧ����Ϊ
�ĵ��Ӧ����Ϊ![]() �����Է���
�����Է���![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ��
��
�� 2���ⲻ��ʽ![]() �����������ҳ�
�����������ҳ�![]() �Ľ⣨��ͼ������Ϊ�������ϵ�
�Ľ⣨��ͼ������Ϊ�������ϵ�![]() ��Ӧ�ĵ�ľ������
��Ӧ�ĵ�ľ������![]() �ĵ��Ӧ����Ϊ
�ĵ��Ӧ����Ϊ![]() ��
��![]() �����Է���
�����Է���![]() �Ľ�Ϊ
�Ľ�Ϊ![]() ��
��![]() ����˲���ʽ
����˲���ʽ![]() �Ľ⼯Ϊ
�Ľ⼯Ϊ![]() ��
��![]() ��
��
�ο��Ķ����ϣ�����������⣺
��1������![]() �Ľ�Ϊ ��
�Ľ�Ϊ ��
��2���ⲻ��ʽ��![]() ��
��
��3���ⲻ��ʽ����

���𰸡���1��x=2��x=-8����2��-1��x��5����3��x��5��x��-3.
��������
��1�������������ϵ�-3��Ӧ�ĵ�ľ������5�ĵ�Ķ�Ӧ����Ϊ2��-8��⼴�ɣ�
��2�������![]() �Ľ⣬�����
�Ľ⣬�����![]() �Ľ⼯���ɣ�
�Ľ⼯���ɣ�
��3�������������ҳ�![]() �Ľ⣬���ɵó�
�Ľ⣬���ɵó�![]() �Ľ⼯.
�Ľ⼯.
�⣺��1�����������ϵ�-3��Ӧ�ĵ�ľ������5�ĵ�Ķ�Ӧ����Ϊ2��-8
���![]() �Ľ�Ϊx=2��x=-8
�Ľ�Ϊx=2��x=-8
��2�����������ϵ�2��Ӧ�ĵ�ľ������3�ĵ�Ķ�Ӧ����Ϊ-1��5
���![]() �Ľ�Ϊx=-1��x=5
�Ľ�Ϊx=-1��x=5
��![]() �Ľ⼯Ϊ-1��x��5.
�Ľ⼯Ϊ-1��x��5.
��3���ɾ���ֵ�ļ��������֪������![]() �������������ϵ�4��-2��Ӧ�ĵ�ľ���֮�͵���8�ĵ��Ӧ��x��ֵ.
�������������ϵ�4��-2��Ӧ�ĵ�ľ���֮�͵���8�ĵ��Ӧ��x��ֵ.
����������4��-2��Ӧ�ĵ�ľ�����6
�����㷽�̵�x�ĵ���4���ұ�-2�����
��x��Ӧ�ĵ���4���ұߣ��ɵ�x=5����x��Ӧ�ĵ���-2����ߣ��ɵ�x=-3
���![]() �Ľ�Ϊx=5��x=-3
�Ľ�Ϊx=5��x=-3
��![]() �Ľ⼯Ϊx��5��x��-3.
�Ľ⼯Ϊx��5��x��-3.
�ʴ�Ϊ��1��x=2��x=-8����2��-1��x��5����3��x��5��x��-3.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ�κ���y=��2m+3��x+m-1��
��1��������ͼ��ԭ�㣬��m��ֵ��
��2��������ͼ����y���ϵĽؾ�Ϊ-3����m��ֵ��
��3�����ú�����ֵy���Ա���x���������С����m��ȡֵ��Χ��
��4���ú���ͼ�����ڶ����ޣ���m��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��AB=AC��AE=AF������BF��CE������O������AO����֤��

��1����B=��C
��2��AOƽ����BAC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
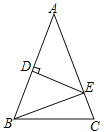
����Ŀ����3�֣���ͼ����ABC�У�AB=AC��AB�Ĵ�ֱƽ���߽���AB��D�㣬����AC��E�㣬����ABC����EBC���ܳ��ֱ���40cm��24cm����AB= cm��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪��A��F��C��D�ĵ���һ��ֱ���ϣ�AF��CD����D����A����AB��DE.�뽫����˵����ABC�ա�DEF�Ĺ��̺����ɲ�������.
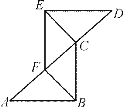
�⣺��AF��CD(______)
��AF��FC��CD��_____����AC��DF��
�ڡ�ABC�͡�DEF�У�AC��______(��֪)����D����A(________)��AB��______(��֪)��
���ABC�ա�DEF(_______)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����1������ͼ��![]() ���ڽ�
���ڽ�![]() ��ƽ�������ڽ�
��ƽ�������ڽ�![]() ��ƽ�����ཻ��
��ƽ�����ཻ��![]() �㣬��̽��
�㣬��̽��![]() ��
��![]() �Ĺ�ϵ����˵�����ɣ�
�Ĺ�ϵ����˵�����ɣ�
����ͼ�ڣ�![]() ���ڽ�
���ڽ�![]() ��ƽ���������
��ƽ���������![]() ��ƽ�����ཻ��
��ƽ�����ཻ��![]() �㣬��̽��
�㣬��̽��![]() ��
��![]() �Ĺ�ϵ����˵�����ɣ�
�Ĺ�ϵ����˵�����ɣ�
��2����ͼ�ۢܣ��ı���![]() �У���
����![]() ��
��![]() ��
��![]() Ϊ�ı���
Ϊ�ı���![]() ���ڽ�
���ڽ�![]() �����
�����![]() ��ƽ��������ֱ���ཻ���гɵ���ǣ������ã�1���еĽ�������������⣺
��ƽ��������ֱ���ཻ���гɵ���ǣ������ã�1���еĽ�������������⣺
����ͼ�ۣ���![]() �Ķ���������
�Ķ��������� ![]() �Ĵ���ʽ��ʾ��
�Ĵ���ʽ��ʾ��
����ͼ�ܣ����ı���![]() ����ֱ��
����ֱ��![]() ���۵õ��ı���
���۵õ��ı���![]() ��
��![]() Ϊ
Ϊ![]() �ӳ�����һ�㣬����
�ӳ�����һ�㣬����![]() ��
��![]() ��
��![]() �Ľ�ƽ���߽��ڵ�
�Ľ�ƽ���߽��ڵ�![]() ����
����![]() ��
��![]() ��������ϵ��
��������ϵ��



�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��Ϊ�Ӵ��������ȣ�ij���ڽ����½���![]() ��
��![]() ���������������������ס�������������תվ������.��֪����תվÿ��Ҫ���100������������תվÿ��Ҫ���80��������
���������������������ס�������������תվ������.��֪����תվÿ��Ҫ���100������������תվÿ��Ҫ���80��������![]() �����������մ���������Ϊ70�֣�
�����������մ���������Ϊ70�֣�![]() �����������մ���������Ϊ110��.�ס�������תվ����
�����������մ���������Ϊ110��.�ס�������תվ����![]() ��
��![]() �������������������˷����±�.
�������������������˷����±�.
���������֣� | �˷ѣ�Ԫ/�֣� | |||
����תվ | ����תվ | ����תվ | ����תվ | |
|
| ______ | 240 | 180 |
| ______ |
| 250 | 160 |
��1�������תվ����![]() ������������������Ϊ
������������������Ϊ![]() �֣�������Ϣ���.
�֣�������Ϣ���.
��2�������˷�Ϊ![]() Ԫ�������˷�
Ԫ�������˷�![]() ��Ԫ������
��Ԫ������![]() ���֣��ĺ�����ϵʽ����д��
���֣��ĺ�����ϵʽ����д��![]() ��ȡֵ��Χ.
��ȡֵ��Χ.
��3�����ס�������תվ������![]() ��
��![]() �����������ٶ�����ʱ�����˷���ʡ����ʡ�����˷��Ƕ��٣�
�����������ٶ�����ʱ�����˷���ʡ����ʡ�����˷��Ƕ��٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���۲�����![]() �����⣺�����������ǣ� ����
�����⣺�����������ǣ� ����
��![]() ��ֱ��
��ֱ��![]() ��
��![]() ��
��![]() �����
�����![]() ��
��![]() ����ô
����ô![]() ��
��
��![]() �������ε������ڽ���������������ǣ�
�������ε������ڽ���������������ǣ�
��![]() ��ƽ�Ʊ任�У������Ӧ�����ɵ����߶�ƽ�У����ߣ�����ȣ�
��ƽ�Ʊ任�У������Ӧ�����ɵ����߶�ƽ�У����ߣ�����ȣ�
��![]() �������ε���Ǻ���
�������ε���Ǻ���![]() ��
��
A.��![]() ����
����![]() ��B.��
��B.��![]() ����
����![]() ��C.��
��C.��![]() ����
����![]() ��D.��
��D.��![]() ����
����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪������![]() ����A����3��0����B����2��3����C��0��3�����䶥��ΪD��
����A����3��0����B����2��3����C��0��3�����䶥��ΪD��
��1���������ߵĽ���ʽ��
��2�����M��1��m������MB+MD��ֵ��Сʱ����m��ֵ��
��3����P����������λ��ֱ��AC�Ϸ���һ�����㣬����APC����������ֵ��
��4���������ߵĶԳ�����ֱ��AC�ཻ�ڵ�N��EΪֱ��AC������һ�㣬����E��EF��ND���������ڵ�F����N��D��E��FΪ������ı����ܷ�Ϊƽ���ı��Σ����ܣ����E�����ꣻ�����ܣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com