
【题目】某公园的门票价格是:成人20元/张,学生10元/张,满40人可购买团体票(票价均打八折).设一个共有x人的旅游团去该公园游玩,其中学生有y人.
(1)用含x,y的式子表示该旅游团应付的门票费;
(2)如果旅游团有47人,其中学生有12人,那么他们应付多少元门票费?
科目:初中数学 来源: 题型:
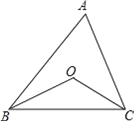
【题目】如图,已知点O是△ABC的两条角平分线的交点,
(1)若∠A=30°,则∠BOC的大小是 ;
(2)若∠A=60°,则∠BOC的大小是 ;
(3)若∠A=n°,则∠BOC的大小是多少?试用学过的知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】八年级(1)班有48名学生,春游前,班长把全班学生对春游地点的意向绘制成了扇形统计图,其中“想去动物园的学生数”的扇形圆心角为60°,则下列说法正确的是( )
A. 想去动物园的学生占全班学生的60% B. 想去动物园的学生有12人
C. 想去动物园的学生肯定最多 D. 想去动物园的学生占全班学生的![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在平面直角坐标系xOy中,抛物线y1=ax2+bx(a≠0),与x轴正半轴交于点A1(2,0),顶点为P1 , △OP1A1为正三角形,现将抛物线y1=ax2+bx(a≠0)沿射线OP1平移,把过点A1时的抛物线记为抛物线y2 , 记抛物线y2与x轴的另一交点为A2;把抛物线y2继续沿射线OP1平移,把过点A2时的抛物线记为抛物线y3 , 记抛物线y3与x轴的另一交点为A3;….;把抛物线y2015继续沿射线OP1平移,把过点A2015时的抛物线记为抛物线y2016 , 记抛物线y2016与x轴的另一交点为A2016 , 顶点为P2016 . 若这2016条抛物线的顶点都在射线OP1上.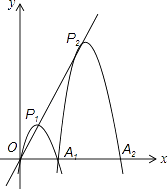
(1)①求△OP1A1的面积;②求a,b的值;
(2)求抛物线y2的解析式;
(3)请直接写出点A2016以及点P2016坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图(一)、图(二)分别为甲、乙两班学生参加投篮测验的投进球数直方图.若甲、乙两班学生的投进球数的众数分别为a、b;中位数分别为c、d,则下列关于a、b、c、d的大小关系,何者正确?( ) 
A.a>b,c>d
B.a>b,c<d
C.a<b,c>d
D.a<b,c<d
查看答案和解析>>
科目:初中数学 来源: 题型:
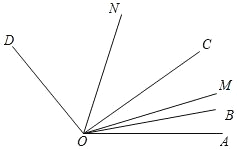
【题目】如图,已知∠AOD=150°,OB、OC、OM、ON 是∠AOD 内的射线,若∠BOC=20°,∠AOB=10°,OM 平分∠AOC,ON 平分∠BOD,当∠BOC 在∠AOD 内绕着点 O以 3°/秒的速度逆时针旋转 t 秒时,当∠AOM:∠DON=3:4 时,则 t=____________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?( )
A.4.5
B.6
C.8
D.9
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD是一张边长为12公分的皮革.皮雕师傅想在此皮革两相邻的角落分别切下△PDQ与△PCR后得到一个五边形PQABR,其中PD=2DQ,PC=RC,且P、Q、
R三点分别在CD、AD、BC上,如图所示.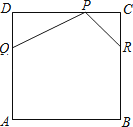
(1)当皮雕师傅切下△PDQ时,若DQ长度为x公分,请你以x表示此时△PDQ的面积.
(2)承(1),当x的值为多少时,五边形PQABR的面积最大?请完整说明你的理由并求出答案.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com