
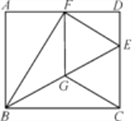
【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,将线段EF绕点F旋转,使点E落在BE上的点G处,连接CG.
(1)证明:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积;
(3)试探究当线段AB与BC满足什么数量关系时,BG=CG,请写出你的探究过程.
【答案】(1)见解析;(2)20;(3)![]()
【解析】试题分析:(1)由折叠得到EF=CE,∠FEG=∠CEG,再加上公共边GE,利用SAS可得出△EFG≌△ECG,利用全等三角形的对应边相等可得出GF=CG,再由FG是线段EF旋转得到的,故FG=EF,等量代换可得出四边形EFGC四条边相等,进而确定出此四边形为菱形;(2)连接FC,与GE交于点O,由折叠得到BF=BC=10,连接FC,交GE于O点,在Rt△ABF中,根据勾股定理求得AF =6,即可得FD=4,设EC=x,则DE=8-x,EF=x,在Rt△FDE中利用勾股定理列出方程42+(8-x)2=x2,解方程得EC=5;在Rt△FDC中根据勾股定理求得FC=4![]() ;在菱形FGCE中FO=
;在菱形FGCE中FO=![]() FC=2
FC=2![]() ,EO=
,EO=![]() GE,GE⊥FC,在在Rt△FOE中求得EO=
GE,GE⊥FC,在在Rt△FOE中求得EO=![]() ,即可得GE=2EO=2
,即可得GE=2EO=2![]() ,从而根据菱形的面积等于两条对角线乘积的一半即可求得菱形的面积;(3)当线段AB与BC满足
,从而根据菱形的面积等于两条对角线乘积的一半即可求得菱形的面积;(3)当线段AB与BC满足![]() 时,BG=CG,理由为:在Rt△ABF中,利用特殊角的三角函数值及锐角三角函数定义求出∠ABF的度数,进而确定出∠FBC的度数,再由折叠得到∠FBE=∠EBC,求出∠EBC为30°,可得出∠BEC为60°,再由GC=CE得到△CGE为等边三角形,再由30°所对的直角边EC等于斜边BE的一半,得到GE为BE的一半,即G为BE的中点,利用直角三角形斜边上的中线等于斜边的一半,得到CG与BG相等都为BE的一半.
时,BG=CG,理由为:在Rt△ABF中,利用特殊角的三角函数值及锐角三角函数定义求出∠ABF的度数,进而确定出∠FBC的度数,再由折叠得到∠FBE=∠EBC,求出∠EBC为30°,可得出∠BEC为60°,再由GC=CE得到△CGE为等边三角形,再由30°所对的直角边EC等于斜边BE的一半,得到GE为BE的一半,即G为BE的中点,利用直角三角形斜边上的中线等于斜边的一半,得到CG与BG相等都为BE的一半.
试题解析:
(1)根据翻折的方法可得:EF=EC,∠FEG=∠CEG,
在△EFG和△ECG中,
∵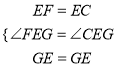 ,
,
∴△EFG≌△ECG(SAS),
∴FG=GC,
∵线段FG是由EF绕F旋转得到的,
∴EF=FG,
∴EF=EC=FG=GC,
∴四边形FGCE是菱形;
(2)连接FC,交GE于O点,
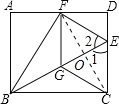
根据折叠可得:BF=BC=10,
∵AB=8,
在Rt△ABF中,
根据勾股定理得:AF=![]() =6,
=6,
∴FD=AD-AF=10-6=4,
设EC=x,则DE=8-x,EF=x,
在Rt△FDE中:FD2+DE2=EF2,即42+(8-x)2=x2,
解得:x=5,
在Rt△FDC中:FD2+DC2=CF2,
则:42+82=FC2,
解得:FC=4![]() ,
,
∵四边形FGCE是菱形,
∴FO=![]() FC=2
FC=2![]() ,EO=
,EO=![]() GE,GE⊥FC,
GE,GE⊥FC,
在Rt△FOE中:FO2+OE2=EF2,即(2![]() )2+EO2=52,
)2+EO2=52,
解得:EO=![]() ,
,
∴GE=2EO=2![]() ,
,
则S菱形CEFG=![]() ×FC×GE=
×FC×GE=![]() ×4
×4![]() ×2
×2![]() =20;
=20;
(3)当![]() 时,BG=CG,理由为:
时,BG=CG,理由为:
由折叠可得:BF=BC,∠FBE=∠CBE,
∵在Rt△ABF中, ![]() ,
,
∴cos∠ABF=![]() ,即∠ABF=30°,
,即∠ABF=30°,
又∵∠ABC=90°,
∴∠FBC=60°,EC=![]() BE,
BE,
∴∠FBE=∠CBE=30°,
∵∠BCE=90°,
∴∠BEC=60°,
又∵GC=CE,
∴△GCE为等边三角形,
∴GE=CG=CE=![]() BE,
BE,
∴G为BE的中点,
则CG=BG=![]() BE.
BE.


科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,对角线BD的垂直平分线MN与AD相交于点M,与BD相交于点N,连接BM,DN.

(1)求证:四边形BMDN是菱形;
(2)若AB=4,AD=8,求MD的长
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校召开运动会,七(1)班学生到超市分两次(第二次少于第一次)购买某种饮料90瓶,共用去205元,已知该种饮料价格如下:
购买瓶数/瓶 | 不超过30 | 30以上不超过50 | 50以上 |
单价/元 | 3 | 2.5 | 2 |
求:两次分别购买这种饮料多少瓶?
查看答案和解析>>
科目:初中数学 来源: 题型:
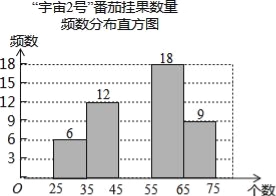
【题目】在太空种子种植体验实践活动中,为了解“宇番2号”番茄,某校科技小组随机调查60株番茄的挂果数量x(单位:个),并绘制如下不完整的统计图表:
“宇番2号”番茄挂果数量统计表
挂果数量x(个) | 频数(株) | 频率 |
25≤x<35 | 6 | 0.1 |
35≤x<45 | 12 | 0.2 |
45≤x<55 | a | 0.25 |
55≤x<65 | 18 | b |
65≤x<75 | 9 | 0.15 |
请结合图表中的信息解答下列问题:
(1)统计表中,a= ,b= ;
(2)将频数分布直方图补充完整;
(3)若绘制“番茄挂果数量扇形统计图”,则挂果数量在“35≤x<45”所对应扇形的圆心角度数为 °;
(4)若所种植的“宇番2号”番茄有1000株,则可以估计挂果数量在“55≤x<65”范围的番茄有 株.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中两条直线为l1:y=–3x+3,l2:y=–3x+9,直线l1交x轴于点A,交y轴于点B,直线l2交x轴于点D,过点B作x轴的平行线交l2于点C,点A、E关于y轴对称,抛物线y=ax2+bx+c过E、B、C三点,下列判断中:
①a–b+c=0;
②2a+b+c=5;
③抛物线关于直线x=1对称;
④抛物线过点(b,c);
⑤S四边形ABCD=5;
其中正确的个数有( )
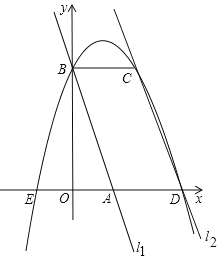
A. 5 B. 4 C. 3 D. 2
查看答案和解析>>
科目:初中数学 来源: 题型:
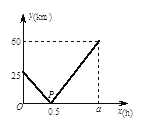
【题目】在一条直线上依次有A、B、C三个海岛,某海巡船从A岛出发沿直线匀速经B 岛驶向C岛,执行海巡任务,最终达到C岛.设该海巡船行驶x(h)后,与B港的距离为y(km),y与x的函数关系如图所示.
(1)填空:A、C两港口间的距离为 km,![]() ;
;
(2)求y与x的函数关系式,并请解释图中点P的坐标所表示的实际意义;
(3)在B岛有一不间断发射信号的信号发射台,发射的信号覆盖半径为15km,求该海巡船能接受到该信号的时间有多长?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(本题10分)如图,直线y=x+m和抛物线y=![]() +bx+c都经过点A(1,0),
+bx+c都经过点A(1,0),
B(3,2).
(1)求m的值和抛物线的解析式;
(2)求不等式x2+bx+c>x+m的解集.(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】体育课上,老师为了解女学生定点投篮的情况,随机抽取8名女生进行每人4次定点投篮的测试,进球数的统计如图所示.
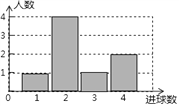
(1)求女生进球数的平均数、中位数;
(2)投球4次,进球3个以上(含3个)为优秀,全校有女生1200人,估计为“优秀”等级的女生约为多少人?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com