
����Ŀ����һ��ֱ����������A��B��C����������ij��Ѳ����A��������ֱ�����پ�B ��ʻ��C����ִ�к�Ѳ�������մﵽC������ú�Ѳ����ʻx��h������B�۵ľ���Ϊy��km����y��x�ĺ�����ϵ��ͼ��ʾ��
��1����գ�A��C���ۿڼ�ľ���Ϊ km��![]() ��
��
��2����y��x�ĺ�����ϵʽ���������ͼ�е�P����������ʾ��ʵ�����壻
��3����B����һ����Ϸ����źŵ��źŷ���̨��������źŸ��ǰ뾶Ϊ15km����ú�Ѳ���ܽ��ܵ����źŵ�ʱ���ж��
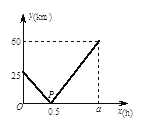
���𰸡���1��85��1.7h��(2) ��0��![]() ��0.5ʱ��y��x�ĺ�����ϵʽΪ��y=-50x+25����0.5��
��0.5ʱ��y��x�ĺ�����ϵʽΪ��y=-50x+25����0.5��![]() ��1.7ʱ��y��x�ĺ�����ϵʽΪ��y=50x��25��(3)�ú�Ѳ���ܽ��ܵ����źŵ�ʱ�� 0.6��h��
��1.7ʱ��y��x�ĺ�����ϵʽΪ��y=50x��25��(3)�ú�Ѳ���ܽ��ܵ����źŵ�ʱ�� 0.6��h��
�����������⣨1����A��B��B��C��ľ�����Ӽ��ɵõ�A��C�����ۿڼ�ľ��룬�������Ѳ�����ٶȣ�Ȼ�����ʱ��=·�����ٶȣ����㼴�����aֵ��
��2����0��x��0.5��0.5��x��1.7���Σ����ô���ϵ������һ�κ�������ʽ��⼴�ɣ�
��3�����ݺ�������ʽ�������Ϊ15kmʱ��ʱ�䣬Ȼ��������ɵý⣮
����������⣺��1����ͼ��֪��A��B�ۿڼ�ľ���Ϊ25��B��C�ۿڼ�ľ���Ϊ60�����ԣ�A��C�ۿڼ�ľ���Ϊ��25+60=85km����Ѳ�����ٶ�Ϊ��25��0.5=50km/h����a=85��50=1.7h��
�ʴ�Ϊ��85��1.7h��
��2����0��x��0.5ʱ����y��x�ĺ�����ϵʽΪ��y=kx+b��������ͼ���㣨0��25������0.5��0������![]() ����ã�
����ã� ![]() �����ԣ�y=��50x+25��
�����ԣ�y=��50x+25��
��0.5��x��1.7ʱ����y��x�ĺ�����ϵʽΪ��y=mx+n��������ͼ���㣨0.5��0������1.7��60������![]() ����ã�
����ã� ![]() �����ԣ�y=50x��25��
�����ԣ�y=50x��25��
��3������50x+25=15�����x=0.2����50x��25=15�����x=0.8��
���ԣ��ú�Ѳ���ܽ��ܵ����źŵ�ʱ��Ϊ��0.6h��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ı���ABCD��ƽ���ı��Σ�E��F�ǶԽ���AC�ϵ����㣬��1=��2��

��1����֤��AE=CF��
��2����֤���ı���EBFD��ƽ���ı��Σ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ǰ����ͨӵ���dz��й�����һ�����⣮���гǶ����ŵĿ�ͨΪ���������������������ڽ�ͨѹ�� ���˹ؼ����ã���Ϊ�˱�֤��ȫ��������������� 80 ǧ��/Сʱ����һ�������£������ϵij��� �ٶ� v����λ��ǧ��/Сʱ���dz����ܶ� x����λ����/ǧ�ף��ĺ����������ϵij����ܶȴﵽ 180 ��/ǧ ��ʱ����ɶ�������ʱ�����ٶ�Ϊ 0���� 0��x��20 ʱ�����ϳ�ͨ���裬�����ٶȶ�Ϊ 80 ǧ��/Сʱ�� �о��������� 20��x��180 ʱ�������ٶ� v �dz����ܶ� x ��һ�κ�����
��1���� 0��x��20 �� 20��x��180 ʱ���ֱ�д������ v ���� x �ĺ�����ϵʽ��
��2���������ܶ� x Ϊ���ʱ������������λʱ����ͨ������ij�۲��ij���������λ����/Сʱ��w=x��v���Դﵽ���������ֵ��
��3��ij����߷壨7:30��9:30�����������ſ��ƹ��������ϵij����ٶ�ʼ�ձ��� 40 ǧ��/Сʱ�������� ��߷��ڼ���ŷ����˶�������?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ1��OΪֱ��AB��һ�㣬����O������OC����AOC��30������һֱ�����ǰ壨��M��30������ֱ�������ڵ�O����һ��ON������OA�ϣ���һ��OM��OC����ֱ��AB���Ϸ���
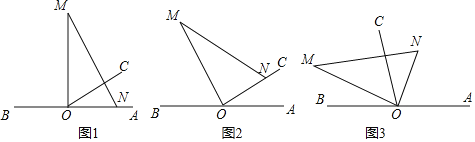
��1����ͼ1�е����ǰ��Ƶ�O��ÿ��5�����ٶ�����ʱ�뷽����תһ�ܣ���ͼ2������t���ON����OC���ϣ���t�����루ֱ��д�������
��2���ڣ�1���������£������ǰ����ת����ͬʱ����OCҲ��O����ÿ��10�����ٶ�����ʱ�뷽����תһ�ܣ���OCת��9��ʱ�����MOC�Ķ�����
��3���ڣ�2���������£����Ǽ����˶�������ʱ����MOC��35������˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
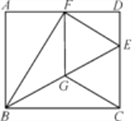
����Ŀ����ͼ���ھ���ABCD�У���EΪCD��һ�㣬����BCE��BE���ۺ��Cǡ������AD���ϵĵ�F�������߶�EF�Ƶ�F��ת��ʹ��E����BE�ϵĵ�G��������CG.
(1)֤�����ı���CEFG�����Σ�
(2)��AB=8��BC=10�����ı���CEFG�������
(3)��̽�����߶�AB��BC����ʲô������ϵʱ��BG=CG����д�����̽�����̣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���Ķ�������ϣ�
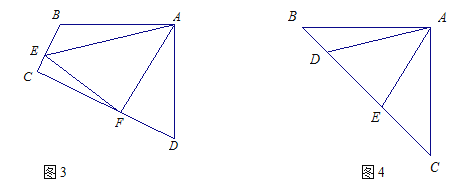
С����������һ�����⣺��ͼ1����E��F�ֱ���������ABCD�ı�BC��CD�ϣ���EAF=45��������EF����EF=BE+DF����˵�����ɣ�

С��������˼���ģ�Ҫ����������⣬����Ӧ��취����Щ��ɢ���߶���Լ��У����Ⱥ����˷��ۡ���ת��ƽ�Ƶķ�����������߶�AB��AD�ǹ��㲢����ȵģ������ҵ��������ķ��������ķ����ǽ���ABE���ŵ�A��ʱ����ת90���õ���ADG��������ȫ�ȵ�֪ʶ�����������⣨��ͼ2����
�ο�С��ͬѧ˼������ķ���������������⣺
��1����ͼ3���ı���ABCD�У�AB=AD����BAD=90����E��F�ֱ��ڱ�BC��CD�ϣ���EAF=45��������B����D������ֱ�ǣ�����B����D����_ ��ϵʱ������EF=BE+DF��
��2����ͼ4������ABC�У���BAC=90����AB=AC����D��E���ڱ�BC�ϣ�����DAE=45������BD=1�� EC=2����DE�ij���
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����Լ���л�����Ĵ�ͳ����.Ϊ���������Լ��ˮ����ʶ,ij�ж�������ˮʵ���������շ������ƶ���������ˮ�շѱ�:ÿ��ÿ�µ���ˮ������![]() ������ʱ��ˮ��Ϊÿ������
������ʱ��ˮ��Ϊÿ������![]() Ԫ,����
Ԫ,����![]() ������ʱ�������IJ��ְ�ÿ������
������ʱ�������IJ��ְ�ÿ������![]() Ԫ�շ�.
Ԫ�շ�.
(1)����ij������9�·���ˮ![]() ������(
������(![]() )��Ӧ��ˮ��
)��Ӧ��ˮ��![]() Ԫ�������ú�
Ԫ�������ú�![]() �Ĵ���ʽ��ʾ
�Ĵ���ʽ��ʾ![]() ;
;
(2)���ij������12�·ݽ�ˮ��![]() Ԫ,��ô����¸û��������˶���������ˮ?
Ԫ,��ô����¸û��������˶���������ˮ?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ϣ����ѧ�Ҷ���ͼ(��Ԫ3-4����)��Ĺ���ϼ����ţ� ��������������֮һ���Ҹ���ͯ�ꣻ�ٻ�����������ʮ����֮һ�����ճ�����ϸϸ�ĺ��룻�����˻飬�ֶȹ���һ�����߷�֮һ���ٹ����꣬�����˶��ӣ��е����Ҹ������Ƕ���ֻ����������ȫ�������һ�룻�����������ڼ��ȱ�ʹ�жȹ������꣬Ҳ����������.��
����������Ϣ�����������
��1������ͼ��������
��2������ͼ��ʼ���ְ�ʱ�����䣻
��3��������ʱ����ͼ������.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ֱ֪��y=kx+b������A��3��7����B����8��-4����
��1����ֱ�ߵĽ���ʽ��
��2�������ֱ����x�ᡢy��Ľ������ꡣ�����ֱ������������Χ�������ε������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com