
【题目】某校召开运动会,七(1)班学生到超市分两次(第二次少于第一次)购买某种饮料90瓶,共用去205元,已知该种饮料价格如下:
购买瓶数/瓶 | 不超过30 | 30以上不超过50 | 50以上 |
单价/元 | 3 | 2.5 | 2 |
求:两次分别购买这种饮料多少瓶?
科目:初中数学 来源: 题型:
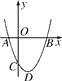
【题目】如图,二次函数y=ax2+bx+c(a>0)的图象的顶点为点D,其图象与x轴的交点A、B的横坐标分别为-1,3,与y轴负半轴交于点C.在下面五个结论中:①2a-b=0;②a+b+c>0;③c=-3a;④只有当a=![]() 时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
时,△ABD是等腰直角三角形;⑤使△ACB为等腰三角形的a的值有4个.其中正确的结论是________(只填序号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】典典同学学完统计知识后,随机调查了她家所在辖区若干名居民的年龄,将调查数据绘制成如下扇形和条形统计图:
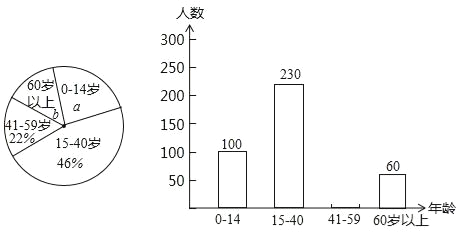
请根据以上不完整的统计图提供的信息,解答下列问题:
(1)扇形统计图中a= ,b= ;并补全条形统计图;
(2)若该辖区共有居民3500人,请估计年龄在0~14岁的居民的人数.
(3)一天,典典知道了辖区内60岁以上的部分老人参加了市级门球比赛,比赛的老人们分成甲、乙两组,典典很想知道甲乙两组的比赛结果,王大爷告诉说,甲组与乙组的得分和为110,甲组得分不低于乙组得分的1.5倍,甲组得分最少为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,甲、乙两人以相同路线前往离学校12千米的地方参加植树活动.分析甲、乙两人前往目的地所行驶的路程S(千米)随时间t(分钟)变化的函数图象,解决下列问题:
(1)求出甲、乙两人所行驶的路程S甲、S乙与t之间的关系式;
(2)甲行驶10分钟后,甲、乙两人相距多少千米?

查看答案和解析>>
科目:初中数学 来源: 题型:
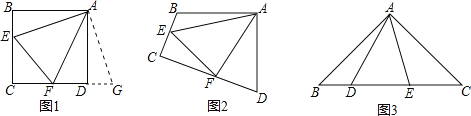
【题目】(1)探究:如图1和2,四边形ABCD中,已知AB=AD,∠BAD=90°,点E、F分别在BC、CD上,∠EAF=45°.
①如图1,若∠B、∠ADC都是直角,把△ABE绕点A逆时针旋转90°至△ADG,使AB与AD重合,则能证得EF=BE+DF,请写出推理过程;
②如图2,若∠B、∠D都不是直角,则当∠B与∠D满足数量关系 时,仍有EF=BE+DF;
(2)拓展:如图3,在△ABC中,∠BAC=90°,AB=AC=2![]() ,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.
,点D、E均在边BC上,且∠DAE=45°.若BD=1,求DE的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】当前,交通拥堵是城市管理的一大难题.我市城东高架桥的开通为分流过境车辆、缓解市内交通压力 起到了关键作用,但为了保证安全,高架桥上最高限速 80 千米/小时.在一般条件下,高架桥上的车流 速度 v(单位:千米/小时)是车流密度 x(单位:辆/千米)的函数,当桥上的车流密度达到 180 辆/千 米时,造成堵塞,此时车流速度为 0;当 0≤x≤20 时,桥上畅通无阻,车流速度都为 80 千米/小时, 研究表明:当 20≤x≤180 时,车流速度 v 是车流密度 x 的一次函数.
(1)当 0≤x≤20 和 20≤x≤180 时,分别写出函数 v 关于 x 的函数关系式;
(2)当车流密度 x 为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)w=x·v可以达到最大,并求出最大值;
(3)某天早高峰(7:30—9:30)经交警部门控制管理,桥上的车流速度始终保持 40 千米/小时,问这天 早高峰期间高架桥分流了多少辆车?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,动点A从原点出发向数轴负方向运动,同时,动点B也从原点出发向数轴正方向运动,3秒后两点相距15个单位长度,已知动点A、B的速度比是1:4(速度单位:1单位长度/秒)。
![]()
(1)求两个动点运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点分别从(1)中标出的位置同时向数轴负方向运动,问经过几秒,原点恰好处在两个动点的正中间?
查看答案和解析>>
科目:初中数学 来源: 题型:
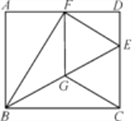
【题目】如图,在矩形ABCD中,点E为CD上一点,将△BCE沿BE翻折后点C恰好落在AD边上的点F处,将线段EF绕点F旋转,使点E落在BE上的点G处,连接CG.
(1)证明:四边形CEFG是菱形;
(2)若AB=8,BC=10,求四边形CEFG的面积;
(3)试探究当线段AB与BC满足什么数量关系时,BG=CG,请写出你的探究过程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,四边形OBCD是正方形,且D(0,2),点E是线段OB延长线上一点,M是线段OB上一动点(不包括点O、B),作MN⊥DM,垂足为M,交∠CBE的平分线于点N.
(1)写出点C的坐标;
(2)求证:MD=MN;
(3)连接DN交BC于点F,连接FM,下列两个结论:①FM的长度不变;②MN平分∠FMB,其中只有一个结论是正确的,请你指出正确的结论,并给出证明

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com