
【题目】如图,在等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
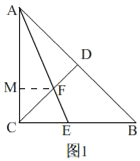
(1)如图1,AE平分∠CAB交BC于E,交CD于F,若DF=2,求AC的长;
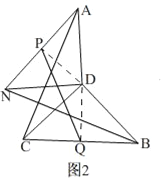
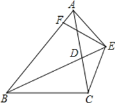
(2)将图1中的△ADC绕点D顺时针旋转一定角度得到△ADN,如图2,P,Q分别为线段AN,BC的中点,连接AC,BN,PQ,求证:BN=![]() PQ;
PQ;
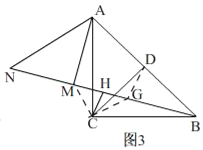
(3)如图3,将△ADC绕点A顺时针旋转一定角度到△AMN,其中D的对应点是M,C的对应点是N,若B,M,N三点在同一直线上,H为BN中点,连接CH,猜想BM,MN,CH之间的数量关系,请直接写出结果.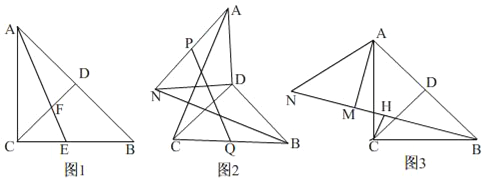
【答案】(1)AC=4+2![]() ;(2)见解析;(3)BM﹣MN=2CH,理由见解析
;(2)见解析;(3)BM﹣MN=2CH,理由见解析
【解析】(1)利用角平分线定理求出FM,再利用等腰直角三角形的性质即可得出CF,最后用AC=![]() CD即可;
CD即可;
(2)先判断出DN:DP=DB:DQ=![]() ,再判断出∠PDQ=∠NDB,进而得出,△PDQ∽△NDB即可判断出结论;
,再判断出∠PDQ=∠NDB,进而得出,△PDQ∽△NDB即可判断出结论;
(3)先判断出,∠MAC=∠GBC进而得出△ACM≌△BCG,即可得出∠ACM=∠BCG,进而△MCG是直角三角形,再用直角三角形的中线得出MG=2CH,最后等量代换即可.
(1)如图1∵等腰直角△ABC中,∠ACB=90°,CA=CB,CD为斜边AB上的中线.
∴CD⊥AB,∠ACD=45°
过点F作FM⊥AC,
∵AE平分∠CAB,
∴FM=FD=2
在Rt△CMF中,∠ACD=45°,
∴CF=![]() MF=2
MF=2![]() ,
,
∴CD=CF+FD=2![]() +2,
+2,
∵CD是等腰直角三角形斜边的中线,
∴AC=![]() CD=
CD=![]() (2
(2![]() +2)=4+2
+2)=4+2![]() ;
;
(2)如图2,连接DP,DQ,
∵△ADC绕点D顺时针旋转一定角度得到△ADN,
∴AN=BC,DN=CD=DB,△ADN是等腰直角三角形,
∵△BCD是等腰直角三角形,点Q是BC中点,
∴DQ=![]() BC=
BC=![]() ×
×![]() BD=
BD=![]() DN,
DN,
∵点P是AN中点,
∴DP=![]() AN=
AN=![]() BC=DQ,
BC=DQ,
∴![]() =
=![]() ,
,
∵∠NDP=∠CDQ=45°,
∴∠PDQ=∠PDN+∠CDN+∠CDQ=90°+∠CDN,
∵∠NDB=∠CDN+∠CDB=90°+∠CDN,
∴∠PDQ=∠NDB,
∵![]() =
=![]() ,
,
∴△PDQ∽△NDB,
∴![]() =
=![]() ,
,
∴BN=![]() PQ.
PQ.
(3)BM﹣MN=2CH.
理由:如图3,在BN上截取BG=BD,连接CG,CM,
∵△ADC绕点A顺时针旋转一定角度到△AMN,
∴MN=AM=AD=CD=DB,
∴MN=AM=BG,
根据三角形的内角和,得∠MAC=∠GBC,
在△ACM和△BCG中,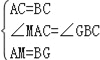 ,
,
∴△ACM≌△BCG,
∴∠ACM=∠BCG,
∴∠MCG=∠ACM+∠ACG=∠BCG+∠ACG=90°,
∴△MCG是直角三角形,
∵H为BN中点,
∴BH=NH,
∵BG=MN,
∴HG=HM,
在Rt△MCG中,HG=HM,
∴MG=2CH,
∴BM=BG+MG=MN+2CH,
∴BM﹣MN=2CH.


 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案科目:初中数学 来源: 题型:
【题目】电影《我和我的祖国》讲述了新中国成立70年间普通百姓与共和国息息相关的故事.影片上映15天就斩获票房26亿元人民币,口碑票房实现双丰收.据统计,10月8日,该电影在重庆的票房收入为140万元,接下来7天的票房变化情况如下表(正数表示比前一天增加的票房,负数表示比前一天减少的票房):
日期 | 9日 | 10日 | 11日 | 12日 | 13日 | 14日 | 15日 |
票房变化(万元) |
|
| 0 |
|
|
|
|
(1)这7天中,票房收入最多的是10月________日,票房收入最少的是10月________日;
(2)根据上述数据可知,这7天该电影在重庆的平均票房收入为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,BD为△ABC的角平分线,且BD=BC,E为BD延长线上的一点,BE=BA,过E作EF⊥AB,F为垂足.下列结论:①△ABD≌△EBC;②∠BCE+∠BCD=180°;③AD=AE=EC;④BA+BC=2BF;其中正确的是( )
A.①②③B.①③④C.①②④D.①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
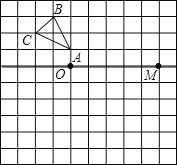
【题目】如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,每个小正方形的顶点叫格点,△ABC的顶点均在格点上,O,M也在格点上.
(1)画出△ABC先向右平移5个单位长度,再向下平移5个单位长度得到的△A'B'C';
(2)画出△ABC关于直线OM对称的△A1B1C1;
(3)画出△ABC绕点O按顺时针方向旋转90°后所得的△A2B2C2;
(4)△A1B1C1与△A2B2C2组成的图形是轴对称图形吗?如果是轴对称图形,请画出对称轴.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】我们新定义一种三角形:若一个三角形中存在两边的平方差等于第三边上高的平方,则称这个三角形为勾股高三角形,两边交点为勾股顶点.
●特例感知
①等腰直角三角形 勾股高三角形(请填写“是”或者“不是”);
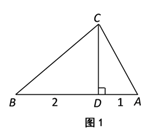
②如图1,已知△ABC为勾股高三角形,其中C为勾股顶点,CD是AB边上的高.若![]() ,试求线段CD的长度.
,试求线段CD的长度.
●深入探究
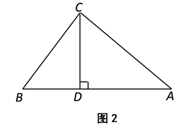
如图2,已知△ABC为勾股高三角形,其中C为勾股顶点且CA>CB,CD是AB边上的高.试探究线段AD与CB的数量关系,并给予证明;
●推广应用
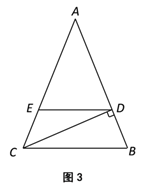
如图3,等腰△ABC为勾股高三角形,其中![]() ,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若
,CD为AB边上的高,过点D向BC边引平行线与AC边交于点E.若![]() ,试求线段DE的长度.
,试求线段DE的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2018年11月2日﹣4日,江西省中小学生研学实践教育推进会和全国中小学综合实践活动(研学实践教育)论坛相继在抚州举行.为拓宽学生视野,引导学生主动适应社会,促进书本知识和生活经验的深度融合,抚州市某中学决定组织部分班级去仙盖山开展研学旅行活动,在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生.参加此次研学旅行活动的老师和学生各有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABC中,∠ACB=90°,AC=6,BC=8,D是AB上一动点,过点D作DE⊥AC于点E,DF⊥BC于点F,连接EF,则线段EF的最小值是( )
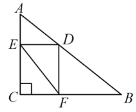
A. 4B. 4.6C. 4.8D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,四边形ABCD是矩形,已知PB=PC.
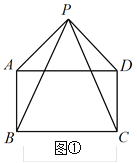
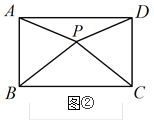
(1)若P是矩形外一点,求证:PA=PD;
(2)若P是矩形边AD(或BC)上的一点,则PA PD;
(3)若点P在矩形ABCD内部,上述结论是否仍然成立?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中∠ACB=90°,CD是AB边上的高,∠BAC的角平分线AF交CD于E,则△CEF必为( )

A.等腰三角形B.等边三角形C.直角三角形D.等腰直角三角形
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com