
【题目】在一个不透明的盒子里装有黑、白两种颜色的球共50个,这些球除颜色外其余完全相同.王颖做摸球试验,搅匀后,她从盒子里随机摸出一个球记下颜色后,再把球放回盒子中,不断重复上述过程,如表是试验中的一组统计数据:
摸球的次数n | 100 | 200 | 300 | 500 | 800 | 1000 | 3000 |
摸到白球的次数m | 65 | 124 | 178 | 302 | 480 | 600 | 1800 |
摸到白球的频率 | 0.65 | 0.62 | 0.593 | 0.604 | 0.6 | 0.6 | 0.6 |
(1)请估计:当n很大时,摸到白球的频率将会接近 ;(精确到0.1)
(2)若从盒子里随机摸出一个球,则摸到白球的概率的估计值为 ;
(3)试估算盒子里黑、白两种颜色的球各有多少个?
【答案】(1)0.6;(2)0.6;(3)盒子里黑颜色的球有20只,盒子白颜色的球有30只
【解析】
(1)观察表格找到逐渐稳定到的常数即可;
(2)概率接近于(1)得到的频率;
(3)白球个数=球的总数×得到的白球的概率,让球的总数减去白球的个数即为黑球的个数,问题得解.
(1)∵摸到白球的频率约为0.6,
∴当n很大时,摸到白球的频率将会接近0.6;
故答案为:0.6;
(2)∵摸到白球的频率为0.6,
∴若从盒子里随机摸出一只球,则摸到白球的概率的估计值为0.6;
(3)黑白球共有20只,
白球为:50×0.6=30(只),
黑球为:50﹣30=20(只).
答:盒子里黑颜色的球有20只,盒子白颜色的球有30只.


 一本好题口算题卡系列答案
一本好题口算题卡系列答案科目:初中数学 来源: 题型:
【题目】春节期间,支付宝“集五福”活动中的“集五福”福卡共分为5种,分别为富强福、和谐福、友善福、爱国福、敬业福,从国家、社会和个人三个层面体现了社会主义核心价值观的价值目标.
(1)小明一家人春节期间参与了支付宝“集五福”活动,小明和姐姐都缺一个“敬业福”,恰巧爸爸有一个可以送给他们其中一个人,两个人各设计了一个游戏,获胜者得到“敬业福”.
在一个不透明盒子里放入标号分别为1,2,3,4的四个小球,这些小球除了标号数字外都相同,将小球摇匀.
小明的游戏规则是:从盒子中随机摸出一个小球,摸到标号数字为奇数小球,则判小明获胜,否则,判姐姐获胜.请判断,此游戏规则对小明和姐姐公平吗?说明理由.
姐姐的游戏规则是:小明从盒子中随机摸出一个小球,记下标号数字后放回盒里,充分摇匀后,姐姐再从盒中随机摸出一个小球,并记下标号数字.若两次摸到小球的标号数字同为奇数或同为偶数,则判小明获胜,若两次摸到小球的标号数字为一奇一偶,则判姐姐获胜.请用列表法或画树状图的方法进行判断此游戏规则对小明和姐姐是否公平.
(2)“五福”中体现了社会主义核心价值观的价值目标的个人层面有哪些?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形ABCD的过长是3,BP=CQ,连接AQ,DP交于点O,并分别与边CD、BC交于点F、E,连接AE.
(1)求证:AQ⊥DP;
(2)求证:AO2=ODOP;
(3)当BP=1时,求QO的长度.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与实践—探究正方形旋转中的数学问题
问题情境:已知正方形![]() 中,点
中,点![]() 在
在![]() 边上,且
边上,且![]() .将正方形
.将正方形![]() 绕点
绕点![]() 顺时针旋转得到正方形
顺时针旋转得到正方形![]() (点
(点![]() ,
,![]() ,
,![]() ,
,![]() 分别是点
分别是点![]() ,
,![]() ,
,![]() ,
,![]() 的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
的对应点).同学们通过小组合作,提出下列数学问题,请你解答.
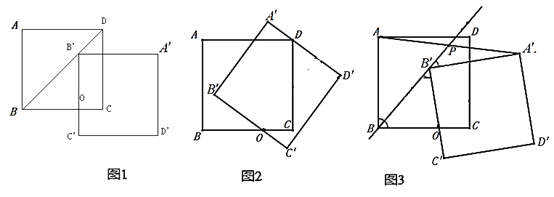
特例分析:(1)“乐思”小组提出问题:如图1,当点![]() 落在正方形
落在正方形![]() 的对角线
的对角线![]() 上时,设线段
上时,设线段![]() 与
与![]() 交于点
交于点![]() .求证:四边形
.求证:四边形![]() 是矩形;
是矩形;
(2)“善学”小组提出问题:如图2,当线段![]() 经过点
经过点![]() 时,猜想线段
时,猜想线段![]() 与
与![]() 满足的数量关系,并说明理由;
满足的数量关系,并说明理由;
深入探究:(3)请从下面![]() ,
,![]() 两题中任选一题作答.我选择题.
两题中任选一题作答.我选择题.
A.在图2中连接![]() 和
和![]() ,请直接写出
,请直接写出![]() 的值.
的值.
B.“好问”小组提出问题:如图3,在正方形![]() 绕点
绕点![]() 顺时针旋转的过程中,设直线
顺时针旋转的过程中,设直线![]() 交线段
交线段![]() 于点
于点![]() .连接
.连接![]() ,并过点
,并过点![]() 作
作![]() 于点
于点![]() .请在图3中补全图形,并直接写出
.请在图3中补全图形,并直接写出![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】光污染是继废气、废水、废渣和噪声等污染之后的一种新的环境污染源,主要包括白亮污染、人工白昼污染和彩光污染,如图,小明家正对面的高楼外墙上安装着一幅巨型广告宣传牌AB,小明想要测量窗外的广告宣传牌AB的高度,他发现晚上家里熄灯后对面楼上的广告宣传牌从A处发出的光恰好从窗户的最高点C处射进房间落在地板上F处,从窗户的最低点D处射进房间向落在地板上E处(B、O、E、F在同一直线E),小明测得窗户距地面的高度OD=1m,窗高CD=1.5m,并测得OE=1m,OF=3m.请根据以上测量数据,求广告宣传牌AB的高度.

查看答案和解析>>
科目:初中数学 来源: 题型:
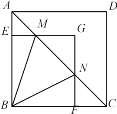
【题目】如图,正方形ABCD边长为3,M、N在对角线AC上且∠MBN=45°,作ME⊥AB于点E、NF⊥BC于点F,反向延长ME、NF交点G,则GEGF的值是( )
A.3B.3![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中
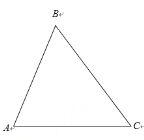
(1)请你利用无刻度的直尺和圆规在平面内画出满足PB2+PC2=BC2的所有点P构成的图形,并在所作图形上用尺规确定到边AC、BC距离相等的点P.(作图必须保留作图痕迹)
(2)在(1)的条件下,连接BP,若BC=15,AC=14,AB=13,求BP的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
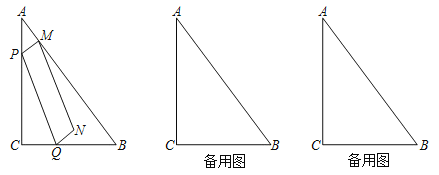
【题目】如图,已知在Rt△ABC中,∠C=90°,AC=8,BC=6,点P、Q分别在边AC、射线CB上,且AP=CQ,过点P作PM⊥AB,垂足为点M,联结PQ,以PM、PQ为邻边作平行四边形PQNM,设AP=x,平行四边形PQNM的面积为y.
(1)当平行四边形PQNM为矩形时,求∠PQM的正切值;
(2)当点N在△ABC内,求y关于x的函数解析式,并写出它的定义域;
(3)当过点P且平行于BC的直线经过平行四边形PQNM一边的中点时,直接写出x的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
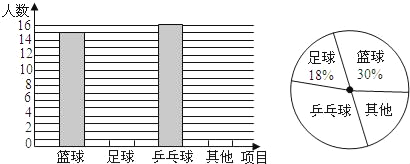
【题目】在大课间活动中,同学们积极参加体育锻炼,小明就本班同学“我最喜爱的体育项目”进行了一次调查统计,下面是他通过收集数据后,绘制的两幅不完整的统计图.请你根据图中提供的信息,解答以下问题:
(1)该班共有_____名学生;
(2)补全条形统计图;
(3)在扇形统计图中,“乒乓球”部分所对应的圆心角度数为_____;
(4)学校将举办体育节,该班将推选5位同学参加乒乓球活动,有3位男同学(A,B,C)和2位女同学(D,E),现准备从中选取两名同学组成双打组合,用树状图或列表法求恰好选出一男一女组成混合双打组合的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com