
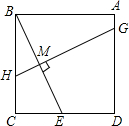
 如图所示,在正方形ABCD中,E为CD的中点,作BE的中垂线GH,垂足为M,则GM:MH的值为( )
如图所示,在正方形ABCD中,E为CD的中点,作BE的中垂线GH,垂足为M,则GM:MH的值为( )| A. | 4:1 | B. | 3:1 | C. | 3:2 | D. | 5:2 |
分析 根据正方形的性质结合全等三角形的判定方法得出△BCE≌△HFG(ASA),则BE=HG,再推出△BHM∽△BEC,进而利用相似三角形的性质得出答案.
解答 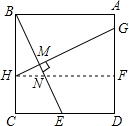 解:过点H作HF⊥AD于点F,交BE于点N,
解:过点H作HF⊥AD于点F,交BE于点N,
由题意可得:∠BHM+∠GHF=90°,
∠HBM+∠BHM=90°,
则∠CBE=∠GHF,
在△BCE和△HFG中,
$\left\{\begin{array}{l}{∠CBE=∠FHG}\\{BC=HF}\\{∠C=∠HFG}\end{array}\right.$,
∴△BCE≌△HFG(ASA),
∴BE=HG,
∵∠BMH=∠C,∠CBE=∠MBH,
∴△BHM∽△BEC,
∵E为CD的中点,
∴$\frac{CE}{BC}$=$\frac{HM}{BM}$=$\frac{1}{2}$,
设HM=x,则BM=2x,故BE=HG=4x,
则MG=4x-x=3x,
故GM:MH的值为:3:1.
故选:B.
点评 此题主要考查了全等三角形的判定与性质以及相似三角形的判定与性质、正方形的性质等知识,正确得出BE=HG是解题关键.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:选择题
| A. | 两条直线被第三条直线所截,同旁内角互补 | |
| B. | 两个锐角之和一定是钝角 | |
| C. | 三角形的任何一个内角大于一个外角 | |
| D. | 内错角相等,两直线平行 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 150元 | B. | 140元 | C. | 130元 | D. | 120元 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,以AD为直径作⊙O,⊙O分别交AB、AC于E、F.
如图,在等腰△ABC中,AB=AC,AD⊥BC,垂足为D,以AD为直径作⊙O,⊙O分别交AB、AC于E、F.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标.(1)以点(3,6)为位似中心,在网格中将△ABC放大,使变换后得到的△A1B1C1与△ABC对应边的比为2:1.请在网格内画出△A1B1C1,并写出点A1的坐标:(-1,4);
如图,方格纸中的每个小方格都是边长为1个单位长度的正方形,△ABC的顶点都在格点上,建立平面直角坐标.(1)以点(3,6)为位似中心,在网格中将△ABC放大,使变换后得到的△A1B1C1与△ABC对应边的比为2:1.请在网格内画出△A1B1C1,并写出点A1的坐标:(-1,4);查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com