
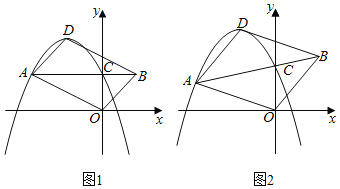
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C.过点C的直线CA与抛物线交于另一点A(点A在对称轴左侧),点B在AC的延长线上,连结OA,OB,DA和DB.
(1)如图1,当AC∥x轴时,
①已知点A的坐标是(﹣2,1),求抛物线的解析式;
②若四边形AOBD是平行四边形,求证:b2=4c.
(2)如图2,若b=﹣2,![]() =
=![]() ,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
【答案】(1)①y=﹣x2﹣2x+1;②证明见解析;(2)存在这样的点A,A(﹣![]() ,
,![]() )
)
【解析】
(1)①由点A(﹣2,1)得到C(0,1),利用待定系数法即可求解;
②作DE⊥x轴于E,交AB于点F,利用顶点坐标及点C的坐标求得DF=![]() ,利用“AAS”证得△AFD≌△BCO,得到DF=OC,即可证得结论;
,利用“AAS”证得△AFD≌△BCO,得到DF=OC,即可证得结论;
(2)由题意知顶点坐标D(﹣1,c+1),设点A(m,﹣m2﹣2m+c),利用“AAS”证得△AFD≌△BCO,作如图的辅助线,证得△ANF∽△AMC,结合已知![]() =
=![]() ,求得
,求得![]() ,利用比例线段即可求解.
,利用比例线段即可求解.
(1)①∵AC∥x轴,点A(﹣2,1),
∴C(0,1),
将点A(﹣2,1),C(0,1)代入抛物线解析式中,得:
![]() ,
,
∴![]() ,
,
∴抛物线的解析式为y=﹣x2﹣2x+1;
②如图1,过点D作DE⊥x轴于E,交AB于点F,
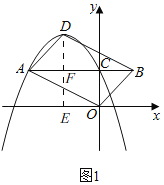
∵AC∥x轴,
∴EF=OC=c,
∵点D是抛物线的顶点坐标,
∴D(![]() ,
,![]() ),
),
∴DF=DE﹣EF=![]() =
=![]() ,
,
∵四边形AOBD是平行四边形,
∴AD=OB,AD∥OB,
∴∠DAF=∠OBC,
∵∠AFD=∠BCO=90°,
∴△AFD≌△BCO(AAS),
∴DF=OC,
∴![]() =c,
=c,
即b2=4c;
(2)如图2,

∵b=﹣2.
∴抛物线的解析式为y=﹣x2﹣2x+c,
∴顶点坐标D(﹣1,c+1),
假设存在这样的点A使四边形AOBD是平行四边形,
设点A(m,﹣m2﹣2m+c)(m<0),
过点D作DE⊥x轴于点E,交AB于F,
∴∠AFD=∠EFC=∠BCO,
∵四边形AOBD是平行四边形,
∴AD=BO,AD∥OB,
∴∠DAF=∠OBC,
∴△AFD≌△BCO(AAS),
∴AF=BC,DF=OC,
过点A作AM⊥y轴于M,交DE于N,
∴DE∥CO,
∴△ANF∽△AMC,
∴![]() =
=![]() ,
,
∵AM=﹣m,AN=AM﹣NM=﹣m﹣1,
∴![]() ,
,
∴![]() ,
,
∴点A的纵坐标为﹣(﹣![]() )2﹣2×(﹣
)2﹣2×(﹣![]() )+c=c﹣
)+c=c﹣![]() <c,
<c,
∵AM∥x轴,
∴点M的坐标为(0,c﹣![]() ),N(﹣1,c﹣
),N(﹣1,c﹣![]() ),
),
∴CM=c﹣(c﹣![]() )=
)=![]() ,
,
∵点D的坐标为(﹣1,c+1),
∴DN=(c+1)﹣(c﹣![]() )=
)=![]() ,
,
∵DF=OC=c,
∴FN=DN﹣DF=![]() ﹣c,
﹣c,
∵![]() =
=![]() ,
,
∴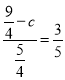 ,
,
∴c=![]() ,
,
∴c﹣![]() =
=![]() ,
,
∴点A纵坐标为![]() ,
,
∴A(﹣![]() ,
,![]() ),
),
∴存在这样的点A,使四边形AOBD是平行四边形.


科目:初中数学 来源: 题型:
【题目】2020年3月,我国湖北省A、B两市遭受严重新冠肺炎影响,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)经过当地政府的大力支持,从D市到B市的运输时间缩短了,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,以△ABC的边AC为直径的⊙O恰为△ABC的外接圆,∠ABC的平分线交⊙O于点D,过点D作DE∥AC交BC的延长线于点E.
(1)求证:DE是⊙O的切线;
(2)若AB=25,BC=![]() ,求DE的长.
,求DE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知在平面直角坐标系xOy中,Rt△OAB的直角顶点B在x轴的正半轴上,点A在第一象限,反比例函数y=![]() (x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是_____.
(x>0)的图象经过OA的中点C.交AB于点D,连结CD.若△ACD的面积是2,则k的值是_____.
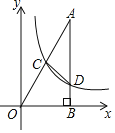
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:点![]() 是
是![]() 轴上一点,将函数
轴上一点,将函数![]() 的图象位于直线
的图象位于直线![]() 右侧部分,以
右侧部分,以![]() 轴为对称轴翻折,得到新的函数
轴为对称轴翻折,得到新的函数![]() 的图象,我们称函数
的图象,我们称函数![]() 是函数
是函数![]() 的相关函数,函数
的相关函数,函数![]() 的图象记作
的图象记作![]() ,函数
,函数![]() 的图象未翻折部分记作
的图象未翻折部分记作![]() ,图象
,图象![]() 和
和![]() 起来记作图象
起来记作图象![]() .
.
例如:函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,它的相关函数
时,它的相关函数![]() 的解析式为
的解析式为![]()
(1)如图,函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,它的相关函数
时,它的相关函数![]() 的解析式为_________;
的解析式为_________;
(2)函数![]() 的解析式为
的解析式为![]() ,当
,当![]() 时,图象
时,图象![]() 上某点的纵坐标为2,求该点的横坐标;
上某点的纵坐标为2,求该点的横坐标;
(3)函数![]() 的解析式为
的解析式为![]() ,
,
①已知点A、B的坐标分别为![]() 、
、![]() ,当
,当![]() 时,且图像
时,且图像![]() 与线段
与线段![]() 只有一个共点时,结合函数图象,求
只有一个共点时,结合函数图象,求![]() 的取值范围;
的取值范围;
②若![]() ,点
,点![]() 是图象
是图象![]() 上任意一点,当
上任意一点,当![]() 时,
时,![]() 的最大值始终保持不变,求
的最大值始终保持不变,求![]() 的取值范围(直接写出结果).
的取值范围(直接写出结果).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D是直径AB延长线上一点,且∠BCE=∠BCD.
(1)求证:CD是⊙O的切线;
(2)若AD=8,![]() =
=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 与反比例函数
与反比例函数![]() 的图象交于A(m,6),B(3,n)两点.
的图象交于A(m,6),B(3,n)两点.
(1)求一次函数的解析式;
(2)求![]() 的面积;
的面积;
(3)根据图象直接写出![]() 的x的取值范围
的x的取值范围

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式变得更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息回答下列问题:
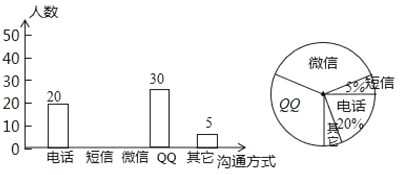
(1)本次调查共调查了______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为______;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com