
【题目】随着通讯技术的迅猛发展,人与人之间的沟通方式变得更多样、便捷.某校数学兴趣小组设计了“你最喜欢的沟通方式”调查问卷(每人必选且只选一种),在全校范围内随机调查了部分学生,将统计结果绘制了如下两幅不完整的统计图,请结合图中所给的信息回答下列问题:
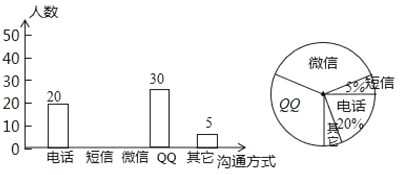
(1)本次调查共调查了______名学生;在扇形统计图中,表示“QQ”的扇形圆心角的度数为______;
(2)将条形统计图补充完整;
(3)该校共有1500名学生,请估计该校最喜欢用“微信”沟通的学生有多少名?
(4)某天甲、乙两名同学都想从“微信”、“QQ”、“电话”三种沟通方式中选一种方式与对方联系,请用列表或画树状图的方法求出甲、乙两名同学恰好选择同一种沟通方式的概率.
【答案】(1)100;108°;(2)补充图形见解析;(3)600人;(4)![]()
【解析】
(1)根据喜欢电话沟通的人数与百分比即可求出共抽查人数,求出使用QQ的百分比即可求出QQ的扇形圆心角度数;
(2)计算出短信与微信的人数即可补全统计图;
(3)用样本中喜欢用微信进行沟通的百分比来估计1500名学生中喜欢用微信进行沟通的人数即可求出答案;
(4)用列表法分别求出所有情况以及甲、乙两名同学恰好选中同一种沟通方式的情况后,利用概念公式即可求出甲、乙两名同学恰好选中同一种沟通方式的概率.
(1)设本次调查共调查了![]() 名学生,其中最喜欢电话沟通方式人数占比=
名学生,其中最喜欢电话沟通方式人数占比=![]() ,解得
,解得![]() ; “QQ”的扇形圆心角的度数=
; “QQ”的扇形圆心角的度数=![]() ;
;
(2)喜欢用短信的人数为:![]() 人,
人,
喜欢用微信的人数为:![]() ,
,
补充图形,如图所示:
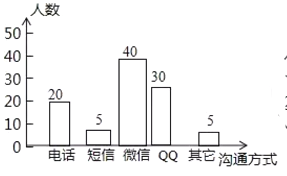
(3)![]() 人
人
(4)有题意,可列表:
2 1 | A | B | C |
A |
|
|
|
B |
|
|
|
C |
|
|
|
所有情况共有9种情况,其中两人恰好选中同一种沟通方式共有3种情况,
甲、乙两名同学恰好选中同一种沟通方式的概率为:![]() .
.


 开心快乐假期作业暑假作业西安出版社系列答案
开心快乐假期作业暑假作业西安出版社系列答案 名题训练系列答案
名题训练系列答案科目:初中数学 来源: 题型:
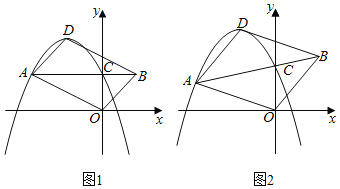
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C.过点C的直线CA与抛物线交于另一点A(点A在对称轴左侧),点B在AC的延长线上,连结OA,OB,DA和DB.
(1)如图1,当AC∥x轴时,
①已知点A的坐标是(﹣2,1),求抛物线的解析式;
②若四边形AOBD是平行四边形,求证:b2=4c.
(2)如图2,若b=﹣2,![]() =
=![]() ,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
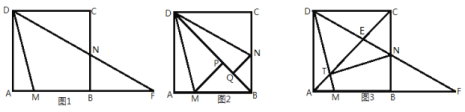
【题目】如图,在正方形ABCD中,点M、N分别在AB、BC边上,∠MDN=45°.
(1)如图1,DN交AB的延长线于点F. 求证:![]() ;
;
(2)如图2,过点M作MP⊥DB于P,过N作NQ⊥BD于![]() ,若
,若![]() ,求对角线BD的长;
,求对角线BD的长;
(3)如图3,若对角线AC交DM,DF分别于点T,E.判断△DTN的形状并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为4的正方形ABCD中,点E为对角线AC上一动点(点E与点A,C不重合),连接DE,作EF⊥DE交射线BA于点F,过点E作MN∥BC分别交CD,AB于点M、N,作射线DF交射线CA于点G.
(1)求证:EF=DE;
(2)当AF=2时,求GE的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中,设二次函数y1=x2+bx+a,y2=ax2+bx+1(a,b是实数,a≠0).
(1)若函数y1的对称轴为直线x=3,且函数y1的图象经过点(a,b),求函数y1的表达式.
(2)若函数y1的图象经过点(r,0),其中r≠0,求证:函数y2的图象经过点(![]() ,0).
,0).
(3)设函数y1和函数y2的最小值分别为m和n,若m+n=0,求m,n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
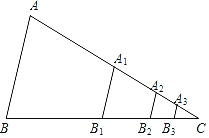
【题目】如图,△ABC的面积为4,分别取AC,BC两边的中点A1,B1,记△A1B1C的面积为S1;再分别取A1C,B1C的中点A2,B2,记△A2B2C的面积为S2,再分别取A2C,B2C的中点A3,B3,记△A3B3C的面积为S3;则S3的值等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )
![]()
A.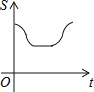 B.
B.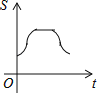
C.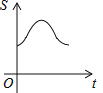 D.
D.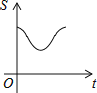
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知函数y= (n为常数).
(n为常数).
(1)当n=1时,
①点P(﹣3,m)在此函数图象上,求m的值.
②当﹣4≤x≤3时,求此函数的最大值和最小值.
(2)当x<n时,若此函数的图象与坐标轴只有两个交点,求n的取值范围.
(3)若n>0,当此函数的图象与以A(0,3)、B(5,﹣2)、C(﹣5,﹣2)、D(﹣5,3)为顶点的四边形的边有且只有四个公共点时,直接写出n的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
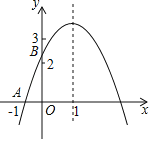
【题目】如图,二次函数y=ax2+bx+c(a≠0)图象与x轴交于A(﹣1,0),对称轴为直线x=1,与y轴的交点B在(0,2)和(0,3)之间(不包括这两个点),下列结论:
①当﹣1<x<3时,y>0;②﹣1<a<﹣![]() ;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是_____.
;③当m≠1时,a+b>m(am+b);④4ac﹣b2>8a其中正确的结论是_____.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com