
【题目】如图,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D是直径AB延长线上一点,且∠BCE=∠BCD.
(1)求证:CD是⊙O的切线;
(2)若AD=8,![]() =
=![]() ,求CD的长.
,求CD的长.
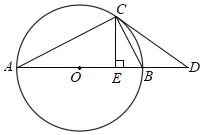
【答案】(1)见解析;(2)4
【解析】
(1)连接OC,根据圆周角定理得到∠ACB=90°,根据余角的性质得到∠A=∠ECB,求得∠A=∠BCD,根据等腰三角形的性质得到∠A=∠ACO,等量代换得到∠ACO=∠BCD,求得∠DCO=90°,于是得到结论;
(2)设BC=k,AC=2k,根据相似三角形的性质即可得到结论.
(1)证明:连接OC,
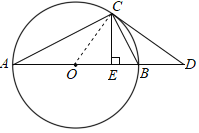
∵AB是⊙O的直径,
∴∠ACB=90°,
∵CE⊥AB,
∴∠CEB=90°,
∴∠ECB+∠ABC=∠ABC+∠CAB=90°,
∴∠A=∠ECB,
∵∠BCE=∠BCD,
∴∠A=∠BCD,
∵OC=OA,
∴∠A=∠ACO,
∴∠ACO=∠BCD,
∴∠ACO+∠BCO=∠BCO+∠BCD=90°,
∴∠DCO=90°,
∴CD是⊙O的切线;
(2)解:∵∠A=∠BCE,
∴tanA=![]() =tan∠BCE=
=tan∠BCE=![]() =
=![]() ,
,
设BC=k,AC=2k,
∵∠D=∠D,∠A=∠BCD,
∴△ACD∽△CBD,
∴![]() =
=![]() =
=![]() ,
,
∵AD=8,
∴CD=4.


科目:初中数学 来源: 题型:
【题目】如图,由两个长为2,宽为1的长方形组成“7”字图形.
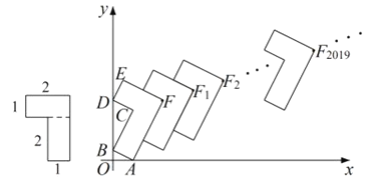
(1)将一个“7”字图形按如图摆放在平面直角坐标系中,记为“7”字图形![]() ,其中顶点
,其中顶点![]() 位于
位于![]() 轴上,顶点
轴上,顶点![]() ,
,![]() 位于
位于![]() 轴上,
轴上,![]() 为坐标原点,则
为坐标原点,则![]() 的值为____.
的值为____.
(2)在(1)的基础上,继续摆放第二个“7”字图形得顶点![]() ,摆放第三个“7”字图形得顶点
,摆放第三个“7”字图形得顶点![]() ,依此类推,…,摆放第
,依此类推,…,摆放第![]() 个“7”字图形得顶点
个“7”字图形得顶点![]() ,…,则顶点
,…,则顶点![]() 的坐标为_____.
的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
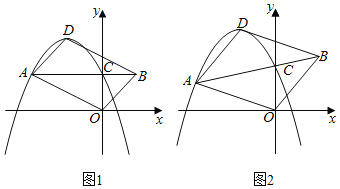
【题目】如图,已知在平面直角坐标系xOy中,抛物线y=﹣x2+bx+c(c>0)的顶点为D,与y轴的交点为C.过点C的直线CA与抛物线交于另一点A(点A在对称轴左侧),点B在AC的延长线上,连结OA,OB,DA和DB.
(1)如图1,当AC∥x轴时,
①已知点A的坐标是(﹣2,1),求抛物线的解析式;
②若四边形AOBD是平行四边形,求证:b2=4c.
(2)如图2,若b=﹣2,![]() =
=![]() ,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
,是否存在这样的点A,使四边形AOBD是平行四边形?若存在,求出点A的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AD=4,将∠A向内翻析,点A落在BC上,记为A1,折痕为DE.若将∠B沿EA1向内翻折,点B恰好落在DE上,记为B1,则AB=_____.
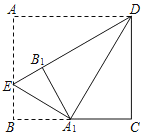
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某学校为了了解本校1200名学生的课外阅读的情况,现从各年级随机抽取了部分学生,对他们一周的课外阅读时间进行了调整,井绘制出如下的统计图①和图②,根据相关信息,解答下列问题:

(Ⅰ)本次接受随机抽样调查的学生人数为______,图①中![]() 的值为______;
的值为______;
(Ⅱ)求本次调查获取的样本数据的众数、中位数和平均数;
(Ⅲ)根据样本数据,估计该校一周的课外阅读时间大于![]() 的学生人数.
的学生人数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点M、N分别在AB、BC边上,∠MDN=45°.
(1)如图1,DN交AB的延长线于点F. 求证:![]() ;
;
(2)如图2,过点M作MP⊥DB于P,过N作NQ⊥BD于![]() ,若
,若![]() ,求对角线BD的长;
,求对角线BD的长;
(3)如图3,若对角线AC交DM,DF分别于点T,E.判断△DTN的形状并说明理由.
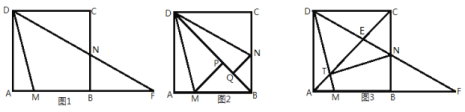
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直角边长为1的等腰直角三角形与边长为2的正方形在同一水平线上,三角形沿水平线从左向右匀速穿过正方形.设穿过时间为t,正方形与三角形不重合部分的面积为s(阴影部分),则s与t的大致图象为( )
![]()
A.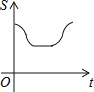 B.
B.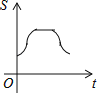
C.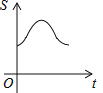 D.
D.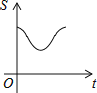
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com