
【题目】如图,![]() 是
是![]() 的直径,点
的直径,点![]() 在
在![]() 上(点
上(点![]() 不与
不与![]() ,
,![]() 重合),直线
重合),直线![]() 交过点
交过点![]() 的切线于点
的切线于点![]() ,过点
,过点![]() 作
作![]() 的切线
的切线![]() 交
交![]() 于点
于点![]() .
.
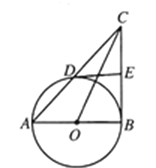
(1)求证:![]() ;
;
(2)若![]() ,求
,求![]() 的值.
的值.
【答案】(1)见解析; (2) ![]() 的值为
的值为![]() .
.
【解析】
(1)证明:连接OD,如图,利用切线长定理得到EB=ED,利用切线的性质得OD⊥DE,AB⊥CB,再根据等角的余角相等得到∠CDE=∠ACB,则EC=ED,从而得到BE=CE;
(2)作OH⊥AD于H,如图,设⊙O的半径为r,先证明四边形OBED为正方形得DE=CE=r,再利用△AOD和△CDE都为等腰直角三角形得到OH=DH= ![]() r,CD=
r,CD= ![]() r,接着根据勾股定理计算出OC=
r,接着根据勾股定理计算出OC=![]() r,然后根据正弦的定义求解.
r,然后根据正弦的定义求解.
解:(1)连接![]() ,如图.
,如图.
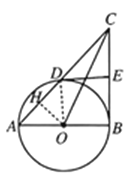
![]() 为
为![]() 的切线,.
的切线,.
∴![]() ,
,![]() ,.
,.
![]() ,
,![]()
![]() ,
,
![]() .
.
![]() .
.
![]() .
.
![]()
(2)如图,作![]() 于点
于点![]() .
.
设![]() 的半径为
的半径为![]() ,
,
![]() ,
,
![]()
∴四边形![]() 为矩形,
为矩形,
又![]() ,
,
∴四边形![]() 为正方形
为正方形
![]() .
.
易得![]() 和
和![]() 都为等腰直角三角形.
都为等腰直角三角形.
![]()
在![]() 中,
中,![]()
在![]() 中,
中,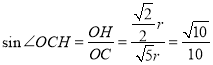
即![]() 的值为
的值为![]() .
.


 各地期末复习特训卷系列答案
各地期末复习特训卷系列答案 小博士期末闯关100分系列答案
小博士期末闯关100分系列答案科目:初中数学 来源: 题型:
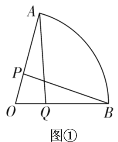
【题目】在扇形![]() 中,
中,![]() ,半径
,半径![]() ,点P为
,点P为![]() 上任一点(不与A、O重合).
上任一点(不与A、O重合).
(1)如图①,Q是![]() 上一点,若
上一点,若![]() ,求证:
,求证:![]() .
.
(2)如图②,将扇形沿![]() 折叠,得到O的对称点
折叠,得到O的对称点![]() .
.
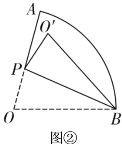
①若点![]() 落在
落在![]() 上,求
上,求![]() 的长;
的长;
②当![]() 与扇形
与扇形![]() 所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
所在的圆相切时,求折痕的长.(注:本题结果不取近似值)
查看答案和解析>>
科目:初中数学 来源: 题型:
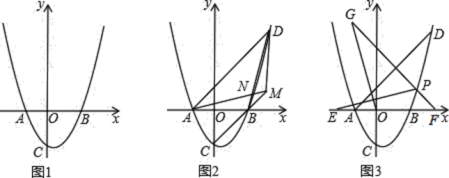
【题目】在平面直角坐标系中,![]() 为坐标原点,抛物线
为坐标原点,抛物线![]() 分别交
分别交![]() 轴正半轴于点
轴正半轴于点![]() ,交
,交![]() 轴负半轴于点
轴负半轴于点![]() ,与
,与![]() 轴负半轴交于点
轴负半轴交于点![]() ,且
,且![]() .
.
(1)如图1,求![]() 的值;
的值;
(2)如图![]() ,
,![]() 是第一象限抛物线上的点,连
是第一象限抛物线上的点,连![]() ,过点
,过点![]() 作
作![]() 轴,交
轴,交![]() 的延长线于点
的延长线于点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,若
,若![]() ,求点
,求点![]() 的坐标以及
的坐标以及![]() 的值;
的值;
(3)如图3,在(2)的条件下,连接![]() ,
,![]() 是第一象限抛物线上的点(点
是第一象限抛物线上的点(点![]() 与点
与点![]() 不重合),过点
不重合),过点![]() 作
作![]() 的垂线,交
的垂线,交![]() 轴于点
轴于点![]() ,点
,点![]() 在
在![]() 轴上(点
轴上(点![]() 在点
在点![]() 的左侧),
的左侧),![]() ,点
,点![]() 在直线
在直线![]() 上,连接
上,连接![]() 、
、![]() .若
.若![]() ,
,![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
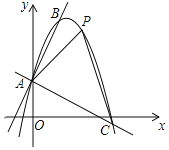
【题目】如图,一个二次函数的图象经过点A(0,1),它的顶点为B(1,3).
(1)求这个二次函数的表达式;
(2)过点A作AC⊥AB交抛物线于点C,点P是直线AC上方抛物线上的一点,当△APC面积最大时,求点P的坐标和△APC的面积最大值.
查看答案和解析>>
科目:初中数学 来源: 题型:
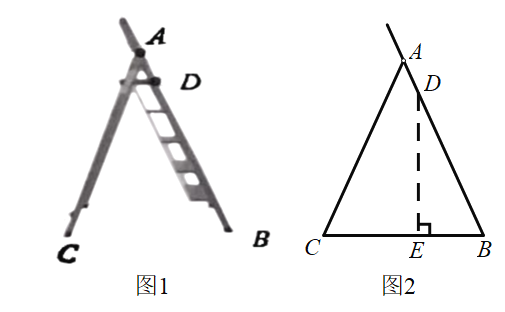
【题目】人字折叠梯完全打开后如图1所示,B,C是折叠梯的两个着地点,D是折叠梯最高级踏板的固定点.图2是它的示意图,AB=AC,BD=140cm,∠BAC=40°,求点D离地面的高度DE.(结果精确到0.1cm;参考数据sin70°≈0. 94,cos70°≈0.34,sin20°≈0.34,cos20°≈0.94)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某超市销售A,B两款保温杯,已知B款保温杯的销售单价比A款保温杯多10元,用480元购买B款保温杯的数量与用360元购买A款保温杯的数量相同.
(1)A,B两款保温杯的销售单价各是多少元?
(2)由于需求量大,A,B两款保温杯很快售完,该超市计划再次购进这两款保温杯共120个,且A款保温杯的数量不少于B保温杯的2倍,A保温杯的售价不变,B款保温杯的销售单价降低10%,两款保温杯的进价每个均为20元,应如何进货才能使这批保温杯的销售利润最大,最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2020年3月,我国湖北省A、B两市遭受严重新冠肺炎影响,邻近县市C、D获知A、B两市分别急需救灾物资200吨和300吨的消息后,决定调运物资支援灾区.已知C市有救灾物资240吨,D市有救灾物资260吨,现将这些救灾物资全部调往A、B两市.已知从C市运往A、B两市的费用分别为每吨20元和25元,从D市运往往A、B两市的费用分别为每吨15元和30元,设从D市运往B市的救灾物资为x吨.
(1)设C、D两市的总运费为w元,求w与x之间的函数关系式,并写出自变量x的取值范围;
(2)经过当地政府的大力支持,从D市到B市的运输时间缩短了,运费每吨减少m元(m>0),其余路线运费不变.若C、D两市的总运费的最小值不小于10320元,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
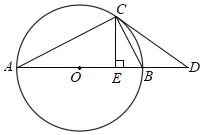
【题目】如图,AB是⊙O的直径,C为⊙O上一点,连接AC,CE⊥AB于点E,D是直径AB延长线上一点,且∠BCE=∠BCD.
(1)求证:CD是⊙O的切线;
(2)若AD=8,![]() =
=![]() ,求CD的长.
,求CD的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com