【题目】已知： ， 与成正比例， 与成反比例，并且时， ； 时， ．求时， 的值．

解：由与成正比例， 与成反比例，可设， ，又，

所以．把， 代入上式，解得． ．

当时， ．

阅读上述解答过程，其过程是否正确，若不正确，请说明理由，并给出正确的解题过程．

参考答案：

【答案】见解析

【解析】试题分析：两个函数比例系数不同，在设的过程中应该体现出来.由于y1与x成正比例，y2与x成反比例，则可以设y1=k1x，y2=（k1≠0，k2≠0），结合题意y=y1+y2，可得y=k1x+；根据题意可把x=1，y=4；x=3，y=5分别代入y=k1x+中，得到一个二元一次方程组，解出k1、k2的值，至此可得y与x的函数关系式；

根据所得的解析式，再将x=4代入其中，至此可求出y的值.

试题解析：其解答过程是错误的。

∵正比例函数y1=k1x，与反比例函数y2= x的k值不一定相等，故设y1=k1x，y2=（k1≠0，k2≠0）.

∵y=y1+y2，

∴y=k1x+.

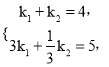把， 的值代入得解得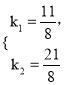

．

∴当x=4时，y=．

关闭