
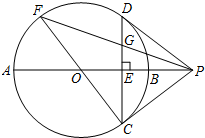
 如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O 的切线,交AB的延长线于点P,联结PD.
如图,⊙O的直径AB垂直于弦CD,垂足为点E,过点C作⊙O 的切线,交AB的延长线于点P,联结PD.分析 (1)连接OD.欲证PD是⊙O的切线,只需证明OD⊥PD即可;通过全等三角形△COP≌△DOP(SAS)的对应角∠OCP=∠ODP=90°来证明该结论;
(2)作FM⊥AB于点M,先求得∠3=∠APC,从而求得$cos∠3=\frac{CE}{OC}=\frac{4}{5}$,得出CE=4,OE=3,然后证得△OFM≌△OCE,得出FM=CE=4,OM=OE=3.
在Rt△OCE中,$cos∠APC=\frac{PC}{OP}=\frac{4}{5}$,设PC=4k,OP=5k,则OC=3k,进而得出$k=\frac{5}{3}$,从而求得$PE=OP-OE=\frac{16}{3}$,$PM=OP+OM=\frac{34}{3}$,
通过△PGE∽△PFM得出$\frac{GE}{FM}=\frac{PE}{PM}$,即可求得EG的长.
解答 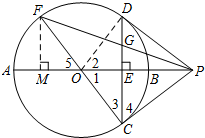 (1)PD与⊙O相切于点D;
(1)PD与⊙O相切于点D;
证明:连接OD
∵在⊙O中,OD=OC,AB⊥CD于点E,
∴∠COP=∠DOP.
在△OCP和△ODP中
$\left\{\begin{array}{l}{OD=OC}\\{∠COP=∠DOP}\\{OP=OP}\end{array}\right.$
∴△OCP≌△ODP(SAS).
∴∠OCP=∠ODP.
又∵PC切⊙O于点C,OC为⊙O半径,
∴OC⊥PC,
∴∠OCP=90°.
∴∠ODP=90°.
∴OD⊥PD于点D.
∴PD与⊙O相切于点D.
(2)作FM⊥AB于点M.
∵∠OCP=90°,CE⊥OP于点E,
∴∠3+∠4=90°,∠APC+∠4=90°.
∴∠3=∠APC.
∵$cos∠APC=\frac{4}{5}$,
∴Rt△OCE中,$cos∠3=\frac{CE}{OC}=\frac{4}{5}$.
∵CF=10,
∴$OF=OC=\frac{1}{2}CF=5$.
∴CE=4,OE=3.
又∵FM⊥AB,AB⊥CD,
∴∠FMO=∠CEO=90°.
在△OFM和△OCE中
$\left\{\begin{array}{l}{∠5=∠1}\\{∠FMO=∠CEO}\\{OF=OC}\end{array}\right.$
∴△OFM≌△OCE(AAS).
∴FM=CE=4,OM=OE=3.
∵在Rt△OCE中,$cos∠APC=\frac{PC}{OP}=\frac{4}{5}$,设PC=4k,OP=5k,
∴OC=3k.
∴3k=5,$k=\frac{5}{3}$.
∴$OP=\frac{25}{3}$.
∴$PE=OP-OE=\frac{16}{3}$,$PM=OP+OM=\frac{34}{3}$.
又∵∠FMO=∠GEP=90°,
∴FM∥GE.
∴△PGE∽△PFM.
∴$\frac{GE}{FM}=\frac{PE}{PM}$,即$\frac{GE}{4}=\frac{{\frac{16}{3}}}{{\frac{34}{3}}}$.
∴$GE=\frac{32}{17}$.
点评 本题考查了切线的判断和性质,三角形全等的判断和性质,相似三角形的判断和性质,直角三角函数等,作出辅助线根据全等三角形是解题的关键.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
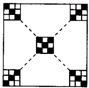 如图,用同样大小的正方形瓷砖铺一块正方形地面,两条对角线铺黑色,其他地方铺白色.铺满这块地面一共用了白色瓷砖100块,那么黑色瓷砖共用了21 块.
如图,用同样大小的正方形瓷砖铺一块正方形地面,两条对角线铺黑色,其他地方铺白色.铺满这块地面一共用了白色瓷砖100块,那么黑色瓷砖共用了21 块.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | A | B. | B | C. | C | D. | D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com