练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    15．如图数轴上有A，B，C，D四点，根据图中各点的位置，所表示的数与11-2$\sqrt{39}$最接近的点是（　　）
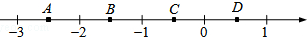
    A．AB．BC．CD．D

    分析 由于$6＜\sqrt{39}＜6.5$，所以$12＜2\sqrt{39}＜13$，所以$-2＜11-2\sqrt{39}＜-1$，因为点B表示的数是-1.5，在-2～-1之间，所以点B最接近．

    解答 解：∵$6＜\sqrt{39}＜6.5$，
    ∴$12＜2\sqrt{39}＜13$，
    ∴$-2＜11-2\sqrt{39}＜-1$，
    ∵点B表示的数是-1.5，在-2～-1之间，
    ∴点B最接近，
    故选：B．

    点评 此题主要考查了估算无理数的大小，可以直接估算所以无理数的值，也可以利用“夹逼法”来估算．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：填空题

    5．已知O为△ABC内角平分线的交点，OD⊥BC于D，∠A=60°，BC=2$\sqrt{3}$，则OD的最大值是1．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

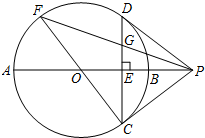    6．如图，⊙O的直径AB垂直于弦CD，垂足为点E，过点C作⊙O 的切线，交AB的延长线于点P，联结PD．
    （1）判断直线PD与⊙O的位置关系，并加以证明；
    （2）联结CO并延长交⊙O于点F，联结FP交CD于点G，如果CF=10，cos∠APC=$\frac{4}{5}$，求EG的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    3．解不等式组：$\left\{\begin{array}{l}2x-4＜0\\ 3（x+1）≥x+2.\end{array}\right.$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    10．阅读下面材料：
    小聪遇到这样一个有关角平分线的问题：如图1，在△ABC中，∠A=2∠B，CD平分∠ACB，AD=2.2，AC=3.6
    求BC的长．
    小聪思考：因为CD平分∠ACB，所以可在BC边上取点E，使EC=AC，连接DE．这样很容易得到△DEC≌△DAC，经过推理能使问题得到解决（如图2）．
    请回答：（1）△BDE是等腰三角形．
    （2）BC的长为5.8．
    参考小聪思考问题的方法，解决问题：
    如图3，已知△ABC中，AB=AC，∠A=20°，BD平分∠ABC，BD=2.3，BC=2．求AD的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：填空题

    20．已知a=98x+98，b=98x+99，c=98x+100，则a2+b2+c2-ab-ac-bc=3．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

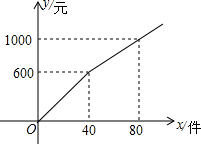    7．某商户以每件8元的价格购进若干件“四季如春植绒窗花”到市场去销售，销售金额y（元）与销售量x（件）的函数关系的图象如图所示，则降价后每件商品销售的价格为（　　）
    A．5元B．10元C．12.5元D．15元

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    4．计算：${（{-\frac{1}{2}}）^{-1}}+\sqrt{{{（{-3}）}^2}}-2sin{30°}+{（{3-π}）^0}$．

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    5．下列各项中叙述正确的是（　　）
    A．若mx=nx，则m=n
    B．若|x|-x=0，则x=0
    C．若mx=nx，则 $\frac{2m}{{x}^{2015}+1}$=$\frac{2n}{{x}^{2015}+1}$
    D．若m=n，则24-mx=24-nx

    查看答案和解析>>

    同步练习册答案