
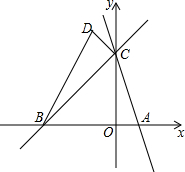
 如图:直线y=-3x+3与x轴交于点A,与y轴交于点C,直线BC与x轴交于B(-3,0),与y轴交于点C.
如图:直线y=-3x+3与x轴交于点A,与y轴交于点C,直线BC与x轴交于B(-3,0),与y轴交于点C.分析 (1)根据直线y=-3x+3与x轴交于点A,与y轴交于点C,分别求出点A与点C的坐标各是多少即可.
(2)首先根据C点的坐标是(0,3),设直线BC的表达式是y=kx+3,然后把B点的坐标代入,求出直线BC的表达式是多少即可.
(3)首先过点D做DP⊥y轴于点P,判断出DP=PC=1,推得∠DCP=45°;然后根据OB=OC=3,∠BOC=90°,推得∠BCO=45°;最后根据∠BCO+∠BCD+∠DCP=180°,求出∠BCD=90°,即可推得△BCD是直角三角形.
(4)在坐标轴上存在点P,使得以P、A、C为顶点的三角形与△BCD相似.然后分三种情况:①当∠APC=90°时;②当∠PAC=90°时;③当∠ACP=90°时;根据三角形相似的判定方法和性质,分别求出P点的坐标各是多少即可.
解答 解:(1)在y=-3x+3中,
当y=0时,x=1,
当x=0时,y=3,
∴A(1,0)、C(0,3).
(2)∵C点的坐标是(0,3),
∴设直线BC的表达式是y=kx+3,
∵B点的坐标是(-3,0),
∴0=-3k+3,
解得k=1,
∴直线BC的表达式:y=x+3.
(3)如图1,过点D做DP⊥y轴于点P,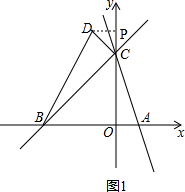 ,
,
∵DP⊥y轴,
∴∠DPC=90°,
∵D(-1,4),C(0,3)
∴DP=PC=1,
∴∠DCP=45°,
又∵C(0,3),B(-3,0)
∴OB=OC=3,
又∵∠BOC=90°,
∴∠BCO=45°,
∵∠BCO+∠BCD+∠DCP=180°,
∴∠BCD=180°-45°-45°=90°,
∴△BCD是直角三角形.
(4)在坐标轴上存在点P,使得以P、A、C为顶点的三角形与△BCD相似.
①如图2,过点D做DP⊥y轴于点P,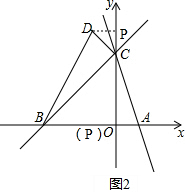 ,
,
由(2),可得
DP=PC=1,∠DPC=90°,
∴DC=$\sqrt{2}$,
∵OB=OC=3,
∴BC=3$\sqrt{2}$,
∵$\frac{AO}{DC}=\frac{1}{\sqrt{2}}=\frac{\sqrt{2}}{2}$,$\frac{CO}{BC}=\frac{3}{3\sqrt{2}}=\frac{\sqrt{2}}{2}$,
∴$\frac{AO}{DC}=\frac{CO}{BC}$,
又∵∠AOC=∠DCB=90°,
∴△AOC∽△DCB,
∴在坐标轴上存在点P(0,0),使得以P、A、C为顶点的三角形与△BCD相似.
②如图3,作AP⊥AC交y轴于点P,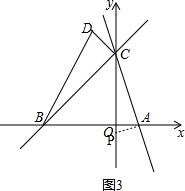 ,
,
∵tan∠CBD=$\frac{DC}{BC}=\frac{\sqrt{2}}{3\sqrt{2}}=\frac{1}{3}$,tan∠0CA=$\frac{AO}{CO}$=$\frac{1}{3}$,
∴tan∠CBD=tan∠OCA,
∴∠CBD=∠OCA,
在△CBD和△∠OCA中,
$\left\{\begin{array}{l}{∠CBD=∠OCA}\\{∠BCD=∠COA}\end{array}\right.$
∴△CBD∽△∠OCA,
∴∠BDC=∠CAO,
在△BCD和△∠CAP中,
$\left\{\begin{array}{l}{∠CBD=∠ACP}\\{∠BCD=∠CAP=90°}\end{array}\right.$
∴△BCD∽△CAP,
∵tan∠OCA=$\frac{1}{3}$,
∴$\frac{AP}{AC}=\frac{1}{3}$,
即$\frac{AP}{\sqrt{{1}^{2}{+3}^{2}}}=\frac{AP}{\sqrt{10}}$=$\frac{1}{3}$,
解得AP=$\frac{\sqrt{10}}{3}$,
∴OP=$\sqrt{{AP}^{2}{-AO}^{2}}$=$\sqrt{{(\frac{\sqrt{10}}{3})}^{2}{-1}^{2}}$=$\frac{1}{3}$,
∴P点的坐标是(0,-$\frac{1}{3}$).
③如图4,作CP⊥AC交x轴于点P,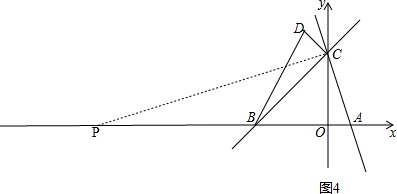 ,
,
在△BCD和△PCA中,
$\left\{\begin{array}{l}{∠BDC=∠PAC}\\{∠BCD=∠PCA=90°}\end{array}\right.$
∴△BCD∽△PCA,
∵∠CPO+∠PCO=90°,∠ACO+∠PCO=90°,
∴∠CPO=∠AC0,
∴tan∠CPO=tan∠AC0=$\frac{AO}{CO}=\frac{1}{3}$,
即$\frac{CO}{PO}=\frac{1}{3}$,
∴$\frac{3}{PO}=\frac{1}{3}$,
解得PO=9,
∴P点的坐标是(-9,0).
综上,可得
P点的坐标是(0,0)、(0,-$\frac{1}{3}$)或(-9,0).
点评 (1)此题主要考查了一次函数综合题,考查了分析推理能力,考查了分类讨论思想的应用,考查了数形结合思想的应用,考查了从已知函数图象中获取信息,并能利用获取的信息解答相应的问题的能力.
(2)此题还考查了三角形相似的判定和性质的应用,要熟练掌握,解答此题的关键是要明确:①三边法:三组对应边的比相等的两个三角形相似;②两边及其夹角法:两组对应边的比相等且夹角对应相等的两个三角形相似;③两角法:有两组角对应相等的两个三角形相似.


科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
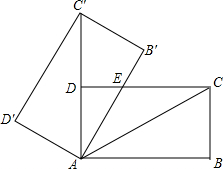 如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为$\sqrt{3}$.
如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置,此时AC′的中点恰好与D点重合,AB′交CD于点E.若AB=3,则△AEC的面积为$\sqrt{3}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
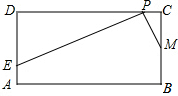 已知:在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C、D 两点).连接PM.过点P作PM的垂线与射线DA相交于点E(如图),设CP=x,DE=y
已知:在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C、D 两点).连接PM.过点P作PM的垂线与射线DA相交于点E(如图),设CP=x,DE=y 查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com