
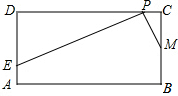
 已知:在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C、D 两点).连接PM.过点P作PM的垂线与射线DA相交于点E(如图),设CP=x,DE=y
已知:在矩形ABCD中,AB=4,BC=2,点M为边BC的中点,点P为边CD上的动点(点P异于C、D 两点).连接PM.过点P作PM的垂线与射线DA相交于点E(如图),设CP=x,DE=y 分析 (1)由矩形的性质和角的互余关系得出∠C=∠D=90°,∠CPM=∠DEP,证明△CPM∽△DEP,得出对应边成比例,即可得出y关于x的函数关系式;
(2)当E与A重合时,DE=DA=2,将y=2代入第一问得出的y与x的关系式中,即可求出x的值;
(3)过P作PH垂直于AB,由对称的性质得到:PD′=PD=4-x,ED′=ED=y=-x2+4x,EA=AD-ED=x2-4x+2,∠PD′E=∠D=90°,在Rt△D′PH中,PH=2,D′P=DP=4-x,根据勾股定理表示出D′H,再由△ED′A∽△D′PH,由相似得比例,将各自表示出的式子代入,可列出关于x的方程,求出方程的解即可得到满足题意的x的值.
解答 解:(1)∵PE⊥PM,∴∠EPM=90°,
∴∠DPE+∠CPM=90°,
又∵四边形ABCD是矩形,
∴∠D=90°,
∴∠DPE+∠DEP=90°,
∴∠CPM=∠DEP,
又∵∠C=∠D=90°,
∴△CPM∽△DEP,
∴$\frac{CP}{DE}$=$\frac{CM}{DP}$,
又∵CP=x,DE=y,AB=DC=4,
∴DP=4-x,
又∵M为BC中点,BC=2,
∴CM=1,
∴$\frac{x}{y}$=$\frac{1}{4-x}$,
∴y=-x2+4x;
(2)当E与A重合时,DE=AD=2,
∵△CPM∽△DEP,
∴$\frac{CP}{DE}$=$\frac{CM}{DP}$,
又∵CP=x,DE=2,CM=1,DP=4-x,
∴$\frac{x}{2}$=$\frac{1}{4-x}$,即x2-4x+2=0,
解得:x=2+$\sqrt{2}$或x=2-$\sqrt{2}$;
(3)存在,过P作PH⊥AB于点H,如图所示: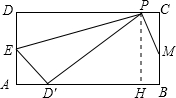 ∵点D关于直线PE的对称点D′落在边AB上,
∵点D关于直线PE的对称点D′落在边AB上,
∴PD′=PD=4-x,ED′=ED=y=-x2+4x,EA=AD-ED=x2-4x+2,∠PD′E=∠D=90°,
在Rt△D′PH中,PH=2,D′P=DP=4-x,
根据勾股定理得:D′H=$\sqrt{(4-x)^{2}-{2}^{2}}$=$\sqrt{{x}^{2}-8x+12}$,
∵∠ED′A=180°-90°-∠PD′H=90°-∠PD′H=∠D′PH,∠PD′E=∠PHD′=90°,
∴△ED′A∽△D′PH,
∴$\frac{ED′}{D′P}$=$\frac{EA}{D′H}$,
即$\frac{-{x}^{2}+4x}{4-x}$=$\frac{x(4-x)}{4-x}$=x=$\frac{{x}^{2}-4x+2}{\sqrt{{x}^{2}-8x+12}}$,
整理得:2x2-4x+1=0,
解得:x=$\frac{2±\sqrt{2}}{2}$,
当x=$\frac{2+\sqrt{2}}{2}$时,y=-($\frac{2+\sqrt{2}}{2}$)2+4×$\frac{2+\sqrt{2}}{2}$=$\frac{5+2\sqrt{2}}{2}$>2,
此时,点E在边DA的延长线上,D关于直线PE的对称点不可能落在边AB上,不合题意舍去;
当x=$\frac{2-\sqrt{2}}{2}$时,y=-($\frac{2-\sqrt{2}}{2}$)2+4×$\frac{2-\sqrt{2}}{2}$=$\frac{5-2\sqrt{2}}{2}$<2,
此时,点E在边AD上,符合题意;
∴当x=$\frac{2-\sqrt{2}}{2}$时,点D关于直线PE的对称点D′落在边AB上.
点评 此题属于相似形综合题,涉及的知识有:相似三角形的判定与性质,对称的性质,矩形的性质,以及一元二次方程的应用,利用了数形结合的数学思想;本题综合性强,难度较大,灵活运用相似三角形的判定与性质是解本题的关键.


科目:初中数学 来源: 题型:解答题
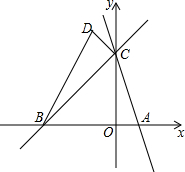 如图:直线y=-3x+3与x轴交于点A,与y轴交于点C,直线BC与x轴交于B(-3,0),与y轴交于点C.
如图:直线y=-3x+3与x轴交于点A,与y轴交于点C,直线BC与x轴交于B(-3,0),与y轴交于点C.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
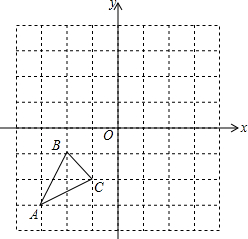 如图,在单位长度为1的方格中,若以点O为坐标原点建立平面直角坐标系,A(-3,-3),B(-2,-1),C(-1,-2).
如图,在单位长度为1的方格中,若以点O为坐标原点建立平面直角坐标系,A(-3,-3),B(-2,-1),C(-1,-2).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
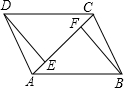 已知,如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.
已知,如图,AB=CD,DE⊥AC,BF⊥AC,E,F是垂足,DE=BF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
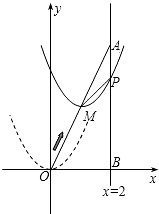 如图,在平面直角坐标系中,已知A点坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.
如图,在平面直角坐标系中,已知A点坐标为(2,4),直线x=2与x轴相交于点B,连结OA,抛物线y=x2从点O沿OA方向平移,与直线x=2交于点P,顶点M到A点时停止移动.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com