
【题目】如图在![]() 中,
中,![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的平分线,
的平分线,![]() 、
、![]() 相交于点
相交于点![]() .
.

(1)请你判断并写出![]() 与
与![]() 之间的数量关系;
之间的数量关系;
(2)试判断线段![]() 、
、![]() 与
与![]() 之间的数量关系并说明理由.
之间的数量关系并说明理由.
 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】弹簧原长(不挂重物)15cm,弹簧总长L(cm)与重物质量x(kg)的关系如下表所示:
弹簧总长L(cm) | 16 | 17 | 18 | 19 | 20 |
重物质量x(kg) | 0.5 | 1.0 | 1.5 | 2.0 | 2.5 |
当重物质量为4kg(在弹性限度内)时,弹簧的总长L(cm)是_________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商厦用8万元购进纪念运动休闲衫,面市后供不应求,商厦又用17.6万元购进了第二批这种衬衫,所购数量是第一批购进数量的2倍,但单价贵了8元,商厦销售这种运动休闲衫时每件定价都是100元,最后剩下的150件按八折销售,很快售完.
(1)商厦第一批和第二批各购进休闲衫多少件?
(2)请问在这两笔生意中,商厦共盈利多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1已知抛物线y=ax2+bx﹣3与x轴相交于A(﹣1,0)、B(3,0),P为抛物线上第四象限上的点.
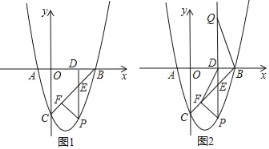
(1)求该抛物线的函数关系式;
(2)如图1,过点P作PD⊥x轴于点D,PD交BC于点E,当线段PE的长度最大时,求点P的坐标.
(3)如图2,当线段PE的长度最大时,作PF⊥BC于点F,连结DF.在射线PD上有一点Q,满足∠PQB=∠DFB,问在坐标轴上是否存在一点R,使得S△RBE=S△QBE?如果存在,直接写出R点的坐标;如果不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=4,BC=3,点E在边AB上,点F在边CD上,点G、H在对角线AC上,若四边形EGFH是菱形,则AE的长是_____.
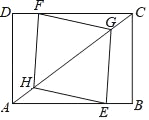
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】绿色生态农场生产并销售某种有机产品,假设生产出的产品能全部售出.如图,线段EF、折线ABCD分别表示该有机产品每千克的销售价y1(元)、生产成本y2(元)与产量x(kg)之间的函数关系.
(1)求该产品销售价y1(元)与产量x(kg)之间的函数关系式;
(2)直接写出生产成本y2(元)与产量x(kg)之间的函数关系式;
(3)当产量为多少时,这种产品获得的利润最大?最大利润为多少?
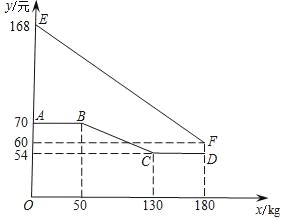
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形网格中,每个小正方形的边长都是1,点A、B、C、D都在格点上.
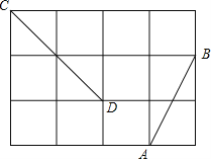
(1)线段AB的长是______;
(2)在图中画出一条线段EF,使EF的长为![]() ,并判断AB、CD、EF三条线段的长能否成为一个直角三角形三边的长?说明理由.
,并判断AB、CD、EF三条线段的长能否成为一个直角三角形三边的长?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形网格中的△ABC,若小方格边长为1,格点△ABC(顶点是网格线交点的三角形)的顶点A,C的坐标分别为(﹣1,1),(0,﹣2),请你根据所学的知识.

(1)在如图所示的网格平面内作出平面直角坐标系;
(2)作出△ABC关于y轴对称的三角形A1B1C1;
(3)判断△ABC的形状,并求出△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com