练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

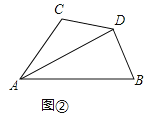
    【题目】如图，平分，且.

    （1）在图1中，当时，求证：；

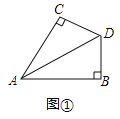
    （2）在图2中，当时，求证：.

    【答案】（1）证明见详解；（2）证明见详解.

    【解析】

    （1）利用AAS判断出△ADC≌△ADB，即可得出结论；

    （2）在AB上截取AE，使得AE=AC，则可证明△ADC≌△ADE，所以有，则可得，即△EDB是等边三角形，即可推出.

    证明：（1）∵∠B+∠C=180°，∠B=90°
    ∴∠C=90°
    ∵AD平分∠BAC
    ∴∠DAC=∠BAD
    ∵AD=AD
    ∴△ACD≌△ABD（AAS）
    ∴BD=CD

    （2）

    如图示，在AB上截取AE，使得AE=AC，

    ∵AD平分∠BAC
    ∴∠DAC=∠BAD
    ∵AD=AD
    ∴△ACD≌△AED（SAS）

    ∴，

    ∵，，

    ∴

    ∴，

    ∴，

    即有：，

    ∴△EDB是等边三角形，

    ∴，

    ∴

    即有：

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】如图1，在矩形ABCD中，动点P从点B出发，沿矩形的边由运动，设点P运动的路程为x，的面积为y，把y看作x的函数，函数的图像如图2所示，则的面积为（ ）

    A. 10 B. 16 C. 18 D. 20

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】下面是小明设计的“作平行四边形ABCD的边AB的中点”的尺规作图过程．

    已知：平行四边形ABCD．

    求作：点M，使点M 为边AB 的中点．

    作法：如图，

    ①作射线DA；

    ②以点A 为圆心，BC长为半径画弧，

    交DA的延长线于点E；

    ③连接EC 交AB于点M ．

    所以点M 就是所求作的点．

    根据小明设计的尺规作图过程，

    (1)使用直尺和圆规，补全图形 (保留作图痕迹)；

    (2)完成下面的证明．

    证明：连接AC，EB．

    ∵四边形ABCD 是平行四边形，

    ∴AE∥BC．

    ∵AE= ，

    ∴四边形EBCA 是平行四边形( )(填推理的依据) ．

    ∴AM =MB ( )(填推理的依据) ．

    ∴点M 为所求作的边AB的中点．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，∠A＝∠B＝90°，E是AB上的一点，且AE＝BC，∠1＝∠2．

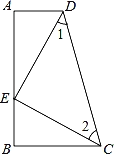
    求证：△CED是等腰直角三角形

    证明：∵∠1＝∠2（　 　）

    ∴EC＝　 　（在一个三角形中，等角对等边）

    ∵∠A＝∠B＝90°，AE＝BC

    ∴△AED≌△BCE（　 　）

    ∴∠AED＝∠　 　（　 　）

    ∵∠BCE+∠BEC＝90°

    ∠　 　+∠BEC＝90°（等量代换）

    ∴∠DEC＝90°．

    ∴△CED是等腰直角三角形．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】有四根长度分别为3，4，5，x（x为正整数）的木棒，从中任取三根，首尾顺次相接都能组成一个三角形则组成的三角形的周长（ ）

    A.最小值是11B.最小值是12C.最大值是14D.最大值是15

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直线AB与x轴交于点C，与y轴交于点B，点A（1，3），点B（0，2）．连接AO

    （1）求直线AB的解析式；

    （2）求三角形AOC的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，△AOB是直角三角形，∠AOB=90°，OB=2OA，点A在反比例函数y=的图象上．若点B在反比例函数y=的图象上，则k的值为（ ）

    A．-4 B．4 C．-2 D．2

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图在中，，、分别是、的平分线，、相交于点．

    （1）请你判断并写出与之间的数量关系；

    （2）试判断线段、与之间的数量关系并说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，方格纸中的每个小方格都是边长为1个单位的正方形，在建立平面直角坐标系后，△ABC的顶点均在格点上，点B的坐标为（1，0）

    （1）在图l中画出△ABC关于x轴对称的△A1B1C1；

    （2）在图2中，以点O为位似中心，将△ABC放大，使放大后的△A2B2C2与△ABC的对应边的比为2：1（画出一种即可）. 直接写出点A的对应点A2的坐标.

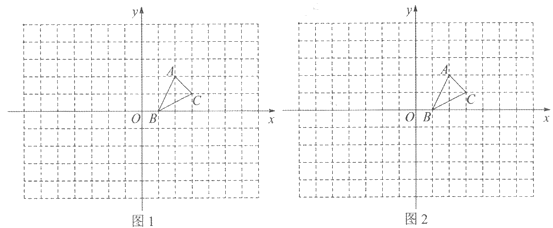
    查看答案和解析>>

    同步练习册答案