
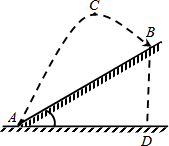
 如图,在高尔夫球赛中,运动员从山坡下A处打出一球向山坡上洞B飞去,已知山坡的坡角为30°,AB=18m,球的飞行的水平距离为9m时达到最大高度12m的C处,若球的飞行轨迹为抛物线,问运动员能否一杆入洞?
如图,在高尔夫球赛中,运动员从山坡下A处打出一球向山坡上洞B飞去,已知山坡的坡角为30°,AB=18m,球的飞行的水平距离为9m时达到最大高度12m的C处,若球的飞行轨迹为抛物线,问运动员能否一杆入洞? 分析 先建立直角坐标系,利用顶点式得到抛物线的解析式,然后求出B点坐标,再判断点B是否在抛物线上即可.
解答 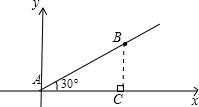 解:建立如图所示的直角坐标系:
解:建立如图所示的直角坐标系:
∵球飞行的水平距离为9米时达最大高度12米,
∴抛物线的顶点坐标为(9,12),
设抛物线的解析式为y=a(x-9)2+12,
把A(0,0)代入得,0=81a+12,解得a=-$\frac{4}{27}$,
∴y=-$\frac{4}{27}$(x-9)2+12,
过B点作BC⊥x轴于C,
∵AB=18,∠BAC=30°,
∴BC=9,AC=$\sqrt{3}$BC,BC=9$\sqrt{3}$,
∴B点坐标为(9$\sqrt{3}$,9),
∵y=9时,9=-$\frac{4}{27}$(x-9)2+12,解得x=$\frac{9}{2}$或$\frac{27}{2}$,
所以点B不在抛物线上,
所以不能一杆进洞.
点评 本题考查了利用二次函数的解析式解决实际问题:先根据题意得到二次函数关系式,把函数值代入解析式得到关于自变量的一元二次方程,解方程,然后根据题意得到问题的解.


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:选择题
| A. | $\sqrt{24}$ | B. | $\sqrt{\frac{3}{2}}$ | C. | $\sqrt{12}$ | D. | $\sqrt{8}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
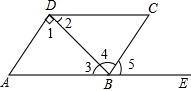 如图,点E在四边形ABCD的边AB的延长线上,下面四个条件中,能判定AB∥CD的是( )
如图,点E在四边形ABCD的边AB的延长线上,下面四个条件中,能判定AB∥CD的是( )| A. | ①③ | B. | ②④ | C. | ①④ | D. | ②③ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com