
ЁОЬтФПЁПГізтГЕЫОЛњаЁЭѕФГЬьЯТЮчгЊдЫЕФТЗЯпШЋЪЧдкЖЋЮїзпЯђЕФДѓЕРЩЯЃЌаЁЭѕДгЕу![]() ГіЗЂЃЌШчЙћЙцЖЈЯђЖЋЮЊе§ЃЌЯђЮїЮЊИКЃЌЫћетЬьЯТЮчЕФааЪЛМЧТМШчЯТЃК+5ЃЌЃ3ЃЌЃ8ЃЌЃ6ЃЌ+10ЃЌЃ6ЃЌ+12ЃЌЃ10ЃЈЕЅЮЛЃКЧЇУзЃЉ
ГіЗЂЃЌШчЙћЙцЖЈЯђЖЋЮЊе§ЃЌЯђЮїЮЊИКЃЌЫћетЬьЯТЮчЕФааЪЛМЧТМШчЯТЃК+5ЃЌЃ3ЃЌЃ8ЃЌЃ6ЃЌ+10ЃЌЃ6ЃЌ+12ЃЌЃ10ЃЈЕЅЮЛЃКЧЇУзЃЉ
ЃЈ1ЃЉНЋзюКѓвЛУћГЫПЭЫЭЕНФПЕФЕиЪБЃЌаЁЭѕОрРыГіЗЂЕу![]() ЪЧЖрЩйЧЇУзЃПдкЕу
ЪЧЖрЩйЧЇУзЃПдкЕу![]() ЕФФФИіЗНЯђЃП
ЕФФФИіЗНЯђЃП
ЃЈ2ЃЉШєЦћГЕКФгЭСПЮЊ![]() Щ§/ЧЇУзЃЌаЁЭѕЫЭЭъзюКѓвЛИіГЫПЭКѓЛиЕНГіЗЂЕу
Щ§/ЧЇУзЃЌаЁЭѕЫЭЭъзюКѓвЛИіГЫПЭКѓЛиЕНГіЗЂЕу![]() ЃЌЙВКФгЭЖрЩйЩ§ЃПЃЈгУКЌ
ЃЌЙВКФгЭЖрЩйЩ§ЃПЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉ
ЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ3ЃЉГізтГЕгЭЯфФкдга12Щ§гЭЃЌЧыЮЪЃКЕБ![]() ЪБЃЌаЁЭѕЭОжаЪЧЗёашвЊМггЭЃПШєашвЊМггЭЃЌжСЩйашвЊМгЖрЩйЩ§гЭЃПШчВЛашвЊЃЌЫЕУїРэгЩЃЎ
ЪБЃЌаЁЭѕЭОжаЪЧЗёашвЊМггЭЃПШєашвЊМггЭЃЌжСЩйашвЊМгЖрЩйЩ§гЭЃПШчВЛашвЊЃЌЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉНЋзюКѓвЛУћГЫПЭЫЭЕНФПЕФЕиЪБЃЌаЁЭѕОрРыГіЗЂЕу![]() ЪЧ6ЧЇУзЃЌдкЕу
ЪЧ6ЧЇУзЃЌдкЕу![]() ЕФЯђЮїЗНЯђЃЛЃЈ2ЃЉаЁЭѕЫЭЭъзюКѓвЛИіГЫПЭКѓЛиЕНГіЗЂЕу
ЕФЯђЮїЗНЯђЃЛЃЈ2ЃЉаЁЭѕЫЭЭъзюКѓвЛИіГЫПЭКѓЛиЕНГіЗЂЕу![]() ЃЌЙВКФгЭ
ЃЌЙВКФгЭ![]() Щ§ЃЛЃЈ3ЃЉаЁЭѕЭОжажСЩйашвЊМг1.2Щ§гЭЃЎ
Щ§ЃЛЃЈ3ЃЉаЁЭѕЭОжажСЩйашвЊМг1.2Щ§гЭЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнЬтвтЃЌНЋИїИігаРэЪ§ЯрМгЃЌШЛКѓИљОне§ИКЪ§ЕФвтвхХаЖЯМДПЩЃЛ
ЃЈ2ЃЉЧѓГіЦћГЕааЪЛЕФзмТЗГЬдйГЫЦћГЕУПЧЇУзЕФКФгЭСПМДПЩЃЛ
ЃЈ3ЃЉНЋ![]() ДњШыЃЈ2ЃЉЕФДњЪ§ЪНжаЃЌШЛКѓКЭ12БШНЯДѓаЁЃЌМДПЩХаЖЯЃЎ
ДњШыЃЈ2ЃЉЕФДњЪ§ЪНжаЃЌШЛКѓКЭ12БШНЯДѓаЁЃЌМДПЩХаЖЯЃЎ
НтЃКЃЈ1ЃЉ![]() ЃЈЧЇУзЃЉ
ЃЈЧЇУзЃЉ
Д№ЃКНЋзюКѓвЛУћГЫПЭЫЭЕНФПЕФЕиЪБЃЌаЁЭѕОрРыГіЗЂЕу![]() ЪЧ6ЧЇУзЃЌдкЕу
ЪЧ6ЧЇУзЃЌдкЕу![]() ЕФЯђЮїЗНЯђЃЎ
ЕФЯђЮїЗНЯђЃЎ
ЃЈ2ЃЉ![]() ЃЈЩ§ЃЉ
ЃЈЩ§ЃЉ
Д№ЃКаЁЭѕЫЭЭъзюКѓвЛИіГЫПЭКѓЛиЕНГіЗЂЕу![]() ЃЌЙВКФгЭ
ЃЌЙВКФгЭ![]() Щ§ЃЎ
Щ§ЃЎ
ЃЈ3ЃЉЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЈЩ§ЃЉ
ЃЈЩ§ЃЉ
Ёп![]()
ЁраЁЭѕЭОжаашвЊМггЭ
![]() ЃЈЩ§ЃЉ
ЃЈЩ§ЃЉ
Д№ЃКаЁЭѕЭОжажСЩйашвЊМг![]() Щ§гЭЃЎ
Щ§гЭЃЎ



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊдіЧПбЇЩњЕФЩэЬхЫижЪЃЌНЬг§ааеўВПУХЙцЖЈбЇЩњУПЬьЛЇЭтЛюЖЏЕФЦНОљЪБМфВЛЩйгк![]() аЁЪБЃЌаЁУїЮЊСЫНтБОАрбЇЩњВЮМгЛЇЭтЛюЖЏЕФЧщПіЃЌЬиНјааСЫЮЪОэЕїВщЃЎ
аЁЪБЃЌаЁУїЮЊСЫНтБОАрбЇЩњВЮМгЛЇЭтЛюЖЏЕФЧщПіЃЌЬиНјааСЫЮЪОэЕїВщЃЎ
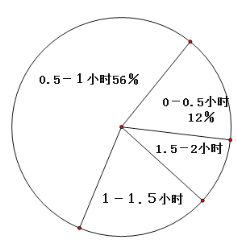
ЃЈ1ЃЉдкНјааЮЪОэЕїВщЪБгаШчЯТВНжшЃЌАДЫГађХХСаЮЊ________ЃЈЬюађКХЃЉЃЎ
ЂйЗЂЮЪОэЃЌШУБЛЕїВщШЫЬюаДЃЛЂкЩшМЦЮЪОэЃЛЂлЖдЮЪОэЕФЪ§ОнНјааЪеМЏгыећРэЃЛ
ЂмЪеЛиЮЪОэЃЛЂнЕУГіНсТлЃЎ
ЃЈ2ЃЉаЁУїИљОнЕїВщНсЙћЃЌОЭБОАрбЇЩњУПЬьВЮМгЛЇЭтЛюЖЏЕФЦНОљЪБМфЛцжЦСЫвдЯТСНЗљВЛЭъећЕФЭГМЦЭМЃЈЭМжа![]() БэЪОДѓгкЕШгк
БэЪОДѓгкЕШгк![]() ЭЌЪБаЁгк
ЭЌЪБаЁгк![]() ЃЌЭМжаРрЫЦЕФМЧКХОљБэЪОетвЛКЌвхЃЉЃЌЧыФуИљОнЭМжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЃЌЭМжаРрЫЦЕФМЧКХОљБэЪОетвЛКЌвхЃЉЃЌЧыФуИљОнЭМжаЬсЙЉЕФаХЯЂНтД№ЯТСаЮЪЬтЃК
ЂйдкетДЮЕїВщжаЙВЕїВщСЫЖрЩйУћбЇЩњЃП
ЂкЭЈЙ§МЦЫуВЙШЋЦЕЪ§ЗжВМжБЗНЭМЃЛ
ЂлЧыФуИљОнвдЩЯЭГМЦНсЙћЃЌОЭбЇЩњВЮМгЛЇЭтЛюЖЏЧщПіЬсГіНЈвщЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЕу![]() дкЪ§жсЩЯЫљЖдгІЕФЪ§ЗжБ№ЪЧ
дкЪ§жсЩЯЫљЖдгІЕФЪ§ЗжБ№ЪЧ![]() ЃЌЦфжа
ЃЌЦфжа![]() Тњзу
Тњзу![]() ЃЎ
ЃЎ
ЃЈ1ЃЉЧѓ![]() ЕФжЕЃЛ
ЕФжЕЃЛ
ЃЈ2ЃЉЪ§жсЩЯгавЛЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() ЃЌЧѓЕу
ЃЌЧѓЕу![]() ЫљЖдгІЕФЪ§ЃЛ
ЫљЖдгІЕФЪ§ЃЛ
ЃЈ3ЃЉЕу![]() ЮЊ
ЮЊ![]() жаЕуЃЌ
жаЕуЃЌ![]() ЮЊдЕуЃЌЪ§жсЩЯгавЛЖЏЕу
ЮЊдЕуЃЌЪ§жсЩЯгавЛЖЏЕу![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФзюаЁжЕМАЕу
ЕФзюаЁжЕМАЕу![]() ЫљЖдгІЕФЪ§ЕФШЁжЕЗЖЮЇЃЎ
ЫљЖдгІЕФЪ§ЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПжЊЪЖСДНгЃК
ЁАзЊЛЏЁЂЛЏЙщЫМЯыЁБЪЧЪ§бЇбЇЯАжаГЃгУЕФвЛжжЬНОПаТжЊЁЂНтОіЮЪЬтЕФЛљБОЕФЪ§бЇЫМЯыЗНЗЈЃЌЭЈЙ§ЁАзЊЛЏЁЂЛЏЙщЁБЭЈГЃПЩвдЪЕЯжЛЏЮДжЊЮЊвбжЊЃЌЛЏИДдгЮЊМђЕЅЃЌДгЖјЪЙЮЪЬтЕУвдНтОі.
ЃЈ1ЃЉЮЪЬтБГОАЃКвбжЊЃКЁїABC.ЪдЫЕУїЃКЁЯA+ЁЯB+ЁЯC=180Ёу.
ЮЪЬтНтОіЃКЃЈЬюГівРОнЃЉ
НтЃКЃЈ1ЃЉШчЭМЂйЃЌбгГЄABЕНEЃЌЙ§ЕуBзїBFЁЮAC.
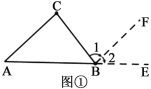
ЁпBFЁЮACЃЈзїЭМЃЉ
ЁрЁЯ1=ЁЯCЃЈ ЃЉ
ЁЯ2=ЁЯAЃЈ ЃЉ
ЁпЁЯ2+ЁЯABC+ЁЯ1=180ЁуЃЈЦННЧЕФЖЈвхЃЉ
ЁрЁЯA+ЁЯABC+ЁЯC=180ЁуЃЈЕШСПДњЛЛЃЉ
аЁНсЗДЫМЃКБОЬтЭЈЙ§ЬэМгЪЪЕБЕФИЈжњЯпЃЌАбШ§НЧаЮЕФШ§ИіНЧжЎКЭзЊЛЏГЩСЫвЛИіЦННЧЃЌРћгУЦННЧЕФЖЈвхЃЌЫЕУїСЫЪ§бЇЩЯЕФвЛИіживЊНсТлЁАШ§НЧаЮЕФШ§ИіФкНЧКЭЕШгк180Ёу.ЁБ
ЃЈ2ЃЉРрБШЬНОПЃКЧыЭЌбЇУЧВЮПМЭМЂкЃЌФЃЗТЃЈ1ЃЉЕФНтОіЙ§ГЬЪдЫЕУїЁАШ§НЧаЮЕФШ§ИіФкНЧКЭЕШгк180ЁуЁБ
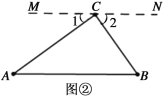
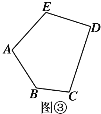
ЃЈ3ЃЉЭиеЙЬНОПЃКШчЭМЂлЃЌЪЧвЛИіЮхБпаЮ,ЧыжБНгаДГіЮхБпаЮABCDEЕФЮхИіФкНЧжЎКЭЁЯA+ЁЯB+ЁЯC+ЁЯD+ЁЯE= .
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
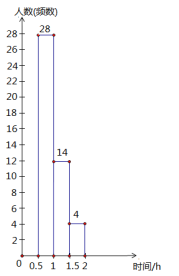
ЁОЬтФПЁПЃЈ9ЗжЃЉвЛСОГізтГЕДгAЕиГіЗЂЃЌдквЛЬѕЖЋЮїзпЯђЕФНжЕРЩЯЭљЗЕЃЌУПДЮааЪЛЕФТЗГЬЃЈМЧЯђЖЋЮЊе§ЃЉМЧТМШчЯТЃЈxЃО9ЧвxЃМ26ЃЌЕЅЮЛЃКkmЃЉ
ЕквЛДЮ | ЕкЖўДЮ | ЕкШ§ДЮ | ЕкЫФДЮ |
x |
| xЉ5 | 2ЃЈ9ЉxЃЉ |
ЃЈ1ЃЉЫЕГіетСОГізтГЕУПДЮааЪЛЕФЗНЯђЃЎ
ЃЈ2ЃЉЧѓОЙ§СЌај4ДЮааЪЛКѓЃЌетСОГізтГЕЫљдкЕФЮЛжУЃЎ
ЃЈ3ЃЉетСОГізтГЕвЛЙВааЪЛСЫЖрЩйТЗГЬЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдФЖСЯТУцВФСЯЃК
аЁУїдкЪ§бЇПЮЭтаЁзщЛюЖЏЪБгіЕНетбљвЛИіЮЪЬтЃК
ШчЙћвЛИіВЛЕШЪНЃЈКЌгаВЛЕШКХЕФЪНзгЃЉжаКЌгаОјЖджЕЃЌВЂЧвОјЖджЕЗћКХжаКЌгаЮДжЊЪ§ЃЌЮвУЧАбетИіВЛЕШЪННазіОјЖджЕВЛЕШЪН.
ЧѓОјЖджЕВЛЕШЪН![]() ЕФНтМЏЃЈТњзуВЛЕШЪНЕФЫљгаНтЃЉ.
ЕФНтМЏЃЈТњзуВЛЕШЪНЕФЫљгаНтЃЉ.
аЁУїЭЌбЇЕФЫМТЗШчЯТЃК
ЯШИљОнОјЖджЕЕФЖЈвхЃЌЧѓГі![]() ЧЁКУЪЧ3ЪБ
ЧЁКУЪЧ3ЪБ![]() ЕФжЕЃЌВЂдкЪ§жсЩЯБэЪОЮЊЕу
ЕФжЕЃЌВЂдкЪ§жсЩЯБэЪОЮЊЕу![]() ЃЌ
ЃЌ![]() ЃЌШчЭМЫљЪО.ЙлВьЪ§жсЗЂЯжЃЌ
ЃЌШчЭМЫљЪО.ЙлВьЪ§жсЗЂЯжЃЌ
![]()
вдЕу![]() ЃЌ
ЃЌ![]() ЮЊЗжНчЕуАбЪ§жсЗжЮЊШ§ВПЗжЃК
ЮЊЗжНчЕуАбЪ§жсЗжЮЊШ§ВПЗжЃК
Еу![]() зѓБпЕФЕуБэЪОЕФЪ§ЕФОјЖджЕДѓгк3ЃЛ
зѓБпЕФЕуБэЪОЕФЪ§ЕФОјЖджЕДѓгк3ЃЛ
Еу![]() ЃЌ
ЃЌ![]() жЎМфЕФЕуБэЪОЕФЪ§ЕФОјЖджЕаЁгк3ЃЛ
жЎМфЕФЕуБэЪОЕФЪ§ЕФОјЖджЕаЁгк3ЃЛ
ЕуBгвБпЕФЕуБэЪОЕФЪ§ЕФОјЖджЕДѓгк3.
вђДЫЃЌаЁУїЕУГіНсТлЃЌОјЖджЕВЛЕШЪН![]() ЕФНтМЏЮЊЃК
ЕФНтМЏЮЊЃК![]() Лђ
Лђ![]() .
.
ВЮееаЁУїЕФЫМТЗЃЌНтОіЯТСаЮЪЬтЃК
ЃЈ1ЃЉЧыФужБНгаДГіЯТСаОјЖджЕВЛЕШЪНЕФНтМЏ.
Ђй![]() ЕФНтМЏЪЧ ЃЛ
ЕФНтМЏЪЧ ЃЛ
Ђк![]() ЕФНтМЏЪЧ .
ЕФНтМЏЪЧ .
ЃЈ2ЃЉЧѓОјЖджЕВЛЕШЪН![]() ЕФНтМЏ.
ЕФНтМЏ.
ЃЈ3ЃЉжБНгаДГіВЛЕШЪН![]() ЕФНтМЏЪЧ ЃЎ
ЕФНтМЏЪЧ ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкЁїABCжаЃЌAB=10ЃЌCA=8ЃЌBC=6ЃЌЁЯBACЕФЦНЗжЯпгыЁЯBCAЕФЦНЗжЯпНЛгкЕуIЃЌЧвDIЁЮBCНЛABгкЕуD,дђDIЕФГЄЮЊ____.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЃЈ1ЃЉЪ§бЇаЁзщгіЕНетбљвЛИіЮЪЬтЃКШєaЃЌbОљВЛЮЊСуЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЧыВЙГфвдЯТНтД№Й§ГЬЃЈжБНгЬюПеЃЉ
ЂйЕБСНИізжФИaЃЌbжага2Иіе§ЃЌ0ИіИКЪБЃЌx= ЃЛЂкЕБСНИізжФИaЃЌbжага1Иіе§ЃЌ1ИіИКЪБЃЌx= ЃЛЂлЕБСНИізжФИaЃЌbжага0Иіе§ЃЌ2ИіИКЪБЃЌx= ЃЛзлЩЯЃЌЕБaЃЌbОљВЛЮЊСуЃЌЧѓxЕФжЕЮЊ ЃЎ
ЃЈ2ЃЉЧыЗТееНтД№Й§ГЬЭъГЩЯТСаЮЪЬтЃК
ЂйШєaЃЌbЃЌcОљВЛЮЊСуЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЂкШєaЃЌbЃЌcОљВЛЮЊСуЃЌЧвa+b+c=0ЃЌжБНгаДГіДњЪ§ЪН![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГаЃвЛЩчЭХЮЊСЫСЫНтЪаЧјГѕжабЇЩњЪгСІБфЛЏЧщПіЃЌДгЪаЧј![]() ФъШыаЃЕФбЇЩњжаЫцЛњГщШЁСЫВПЗжбЇЩњСЌајШ§ФъЕФЪгСІИњзйЕїВщЃЌВЂНЋЪеМЏЕНЕФЪ§ОнНјааећРэЃЌжЦГЩСЫелЯпЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЎ
ФъШыаЃЕФбЇЩњжаЫцЛњГщШЁСЫВПЗжбЇЩњСЌајШ§ФъЕФЪгСІИњзйЕїВщЃЌВЂНЋЪеМЏЕНЕФЪ§ОнНјааећРэЃЌжЦГЩСЫелЯпЭГМЦЭМКЭЩШаЮЭГМЦЭМЃЎ
ЃЈ1ЃЉетДЮНгЪмЕїВщЕФбЇЩњга_____________ШЫЃЛ
ЃЈ2ЃЉЩШаЮЭГМЦЭМжаЁА![]() ЁБЫљЖдгІЕФдВаФНЧгаЖрЩйЖШЃП
ЁБЫљЖдгІЕФдВаФНЧгаЖрЩйЖШЃП
ЃЈ3ЃЉЯжЙцЖЈЪгСІДяЕН![]() МАвдЩЯЮЊКЯИёЃЌШєЪаЧј
МАвдЩЯЮЊКЯИёЃЌШєЪаЧј![]() ФъШыаЃЕФбЇЩњЙВМЦ
ФъШыаЃЕФбЇЩњЙВМЦ![]() ШЫЃЌЧыФуЙРМЦИУНь
ШЫЃЌЧыФуЙРМЦИУНь![]() УћбЇЩњЕФЪгСІдк
УћбЇЩњЕФЪгСІдк![]() ФъгаЖрЩйУћбЇЩњКЯИёЃЎ
ФъгаЖрЩйУћбЇЩњКЯИёЃЎ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com