
ЁОЬтФПЁПЃЈ1ЃЉЪ§бЇаЁзщгіЕНетбљвЛИіЮЪЬтЃКШєaЃЌbОљВЛЮЊСуЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЧыВЙГфвдЯТНтД№Й§ГЬЃЈжБНгЬюПеЃЉ
ЂйЕБСНИізжФИaЃЌbжага2Иіе§ЃЌ0ИіИКЪБЃЌx= ЃЛЂкЕБСНИізжФИaЃЌbжага1Иіе§ЃЌ1ИіИКЪБЃЌx= ЃЛЂлЕБСНИізжФИaЃЌbжага0Иіе§ЃЌ2ИіИКЪБЃЌx= ЃЛзлЩЯЃЌЕБaЃЌbОљВЛЮЊСуЃЌЧѓxЕФжЕЮЊ ЃЎ
ЃЈ2ЃЉЧыЗТееНтД№Й§ГЬЭъГЩЯТСаЮЪЬтЃК
ЂйШєaЃЌbЃЌcОљВЛЮЊСуЃЌЧѓ![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЂкШєaЃЌbЃЌcОљВЛЮЊСуЃЌЧвa+b+c=0ЃЌжБНгаДГіДњЪ§ЪН![]() ЕФжЕЃЎ
ЕФжЕЃЎ
ЁОД№АИЁПЃЈ1ЃЉЂй2ЃЌЂк0ЃЌЂл-2ЃЌ2Лђ0Лђ-2ЃЛЃЈ2ЃЉЂй1Лђ3Лђ-3Лђ-1ЃЛЂк-1Лђ1
ЁОНтЮіЁП
ЃЈ1ЃЉЂйИљОнaЁЂbЕФЗћКЯЛЏМђОјЖджЕМДПЩЕУЕНД№АИЃЛ
ЂкЩшaЪЧе§Ъ§ЃЌbЪЧИКЪ§ЃЌЛЏМђОјЖджЕМДПЩЕУЕНД№АИЃЛ
ЂлИљОнaЁЂbЕФЗћКЯЛЏМђОјЖджЕМДПЩЕУЕНД№АИЃЛ
злКЯЩЯУцШ§ИіЕФНсЙћЕУЕНД№АИЃЛ
ЃЈ2ЃЉЂйЗжЫФжжЧщПіЛЏМђОјЖджЕМДПЩЕУЕНД№АИЃЛ
ЂкИљОнaЁЂbЁЂcОљВЛЮЊСуЃЌЗжСНжжЧщПіЧѓГіД№АИМДПЩ.
ЃЈ1ЃЉЂйЁпaЁЂbЖМЪЧе§Ъ§ЃЌ
Ёр![]() =aЃЌ
=aЃЌ ![]() =bЃЌ
=bЃЌ
Ёр![]() =1+1=2ЃЌ
=1+1=2ЃЌ
ЙЪД№АИЮЊЃК2ЃЛ
ЂкЩшaЪЧИКЪ§ЃЌbЪЧе§Ъ§ЃЌ
Ёр![]() =-aЃЌ
=-aЃЌ![]() =bЃЌ
=bЃЌ
Ёр![]() =-1+1=0ЃЌ
=-1+1=0ЃЌ
ЙЪД№АИЮЊЃК0ЃЛ
ЂлЁпaЁЂbЖМЪЧИКЪ§ЃЌ
Ёр![]() =-aЃЌ
=-aЃЌ ![]() =-bЃЌ
=-bЃЌ
Ёр![]() =-1-1=-2ЃЌ
=-1-1=-2ЃЌ
ЙЪД№АИЮЊЃК-2ЃЛ
злЩЯЃЌЕБaЃЌbОљВЛЮЊСуЃЌЧѓxЕФжЕЮЊ2Лђ0Лђ-2ЃЛ
ЃЈ2ЃЉЂйгЩЬтвтПЩЕУЃКaЁЂbЁЂcЕФЗћКХЗжЮЊЫФжжЧщПіЃК
ЕБaЁЂbЁЂcЖМЪЧе§Ъ§ЪБЃЌ![]() =1+1-1=1ЃЌ
=1+1-1=1ЃЌ
ЕБaЁЂbЁЂcЮЊСНе§вЛИКЧвaЁЂbЮЊе§cЮЊИКЪБЃЌ![]() =1+1+1=3ЃЌ
=1+1+1=3ЃЌ
ЕБaЁЂbЁЂcЮЊвЛе§СНИКЧвaЁЂbЮЊИКcЮЊе§ЪБЃЌ![]() =-1-1-1=-3,
=-1-1-1=-3,
ЕБaЁЂbЁЂcЖМЪЧИКЪ§ЪБЃЌ![]() =-1-1+1=-1ЃЌ
=-1-1+1=-1ЃЌ
злЩЯЃЌ![]() ЕФжЕЮЊ1Лђ3Лђ-3,Лђ-1ЃЛ
ЕФжЕЮЊ1Лђ3Лђ-3,Лђ-1ЃЛ
ЂкЁпaЃЌbЃЌcОљВЛЮЊСуЃЌЧвa+b+c=0ЃЌ
Ёр![]() =
=![]() ЃЌ
ЃЌ
ЁрЕБaЁЂbЁЂcЮЊСНе§вЛИКЪБЃЌ![]() =-1-1+1=-1ЃЌ
=-1-1+1=-1ЃЌ
ЕБaЁЂbЁЂcЮЊвЛе§СНИК![]() =-1+1+1=1ЃЌ
=-1+1+1=1ЃЌ
злЩЯЃЌ![]() ЕФжЕЮЊ-1Лђ1.
ЕФжЕЮЊ-1Лђ1.


 УћаЃПЮЬУЯЕСаД№АИ
УћаЃПЮЬУЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЖЫЮчНкЗХМйЦкМфЃЌФГбЇаЃМЦЛЎзтгУ![]() СОПЭГЕЫЭ
СОПЭГЕЫЭ![]() УћЪІЩњВЮМгбабЇЛюЖЏЃЌЯжгаМзЁЂввСНжжПЭГЕЃЌЫќУЧЕФдиПЭСПКЭзтН№ШчЯТБэЃЌЩшзтгУМзжжПЭГЕ
УћЪІЩњВЮМгбабЇЛюЖЏЃЌЯжгаМзЁЂввСНжжПЭГЕЃЌЫќУЧЕФдиПЭСПКЭзтН№ШчЯТБэЃЌЩшзтгУМзжжПЭГЕ![]() СОЃЌзтГЕзмЗбгУЮЊ
СОЃЌзтГЕзмЗбгУЮЊ![]() дЊЃЎ
дЊЃЎ
МзжжПЭГЕ | ввжжПЭГЕ | |
диПЭСПЃЈШЫ/СОЃЉ |
|
|
зтН№ЃЈдЊ/СОЃЉ |
|
|
ЃЈ1ЃЉЧѓГі![]() ЃЈдЊЃЉгы
ЃЈдЊЃЉгы![]() ЃЈСОЃЉжЎМфКЏЪ§ЙиЯЕЪНЃЛ
ЃЈСОЃЉжЎМфКЏЪ§ЙиЯЕЪНЃЛ
ЃЈ2ЃЉЧѓГіздБфСПЕФШЁжЕЗЖЮЇЃЛ
ЃЈ3ЃЉбЁдёдѕбљЕФзтГЕЗНАИЫљашЕФЗбгУзюЕЭЃПзюЕЭЗбгУЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПГізтГЕЫОЛњаЁЭѕФГЬьЯТЮчгЊдЫЕФТЗЯпШЋЪЧдкЖЋЮїзпЯђЕФДѓЕРЩЯЃЌаЁЭѕДгЕу![]() ГіЗЂЃЌШчЙћЙцЖЈЯђЖЋЮЊе§ЃЌЯђЮїЮЊИКЃЌЫћетЬьЯТЮчЕФааЪЛМЧТМШчЯТЃК+5ЃЌЃ3ЃЌЃ8ЃЌЃ6ЃЌ+10ЃЌЃ6ЃЌ+12ЃЌЃ10ЃЈЕЅЮЛЃКЧЇУзЃЉ
ГіЗЂЃЌШчЙћЙцЖЈЯђЖЋЮЊе§ЃЌЯђЮїЮЊИКЃЌЫћетЬьЯТЮчЕФааЪЛМЧТМШчЯТЃК+5ЃЌЃ3ЃЌЃ8ЃЌЃ6ЃЌ+10ЃЌЃ6ЃЌ+12ЃЌЃ10ЃЈЕЅЮЛЃКЧЇУзЃЉ
ЃЈ1ЃЉНЋзюКѓвЛУћГЫПЭЫЭЕНФПЕФЕиЪБЃЌаЁЭѕОрРыГіЗЂЕу![]() ЪЧЖрЩйЧЇУзЃПдкЕу
ЪЧЖрЩйЧЇУзЃПдкЕу![]() ЕФФФИіЗНЯђЃП
ЕФФФИіЗНЯђЃП
ЃЈ2ЃЉШєЦћГЕКФгЭСПЮЊ![]() Щ§/ЧЇУзЃЌаЁЭѕЫЭЭъзюКѓвЛИіГЫПЭКѓЛиЕНГіЗЂЕу
Щ§/ЧЇУзЃЌаЁЭѕЫЭЭъзюКѓвЛИіГЫПЭКѓЛиЕНГіЗЂЕу![]() ЃЌЙВКФгЭЖрЩйЩ§ЃПЃЈгУКЌ
ЃЌЙВКФгЭЖрЩйЩ§ЃПЃЈгУКЌ![]() ЕФДњЪ§ЪНБэЪОЃЉ
ЕФДњЪ§ЪНБэЪОЃЉ
ЃЈ3ЃЉГізтГЕгЭЯфФкдга12Щ§гЭЃЌЧыЮЪЃКЕБ![]() ЪБЃЌаЁЭѕЭОжаЪЧЗёашвЊМггЭЃПШєашвЊМггЭЃЌжСЩйашвЊМгЖрЩйЩ§гЭЃПШчВЛашвЊЃЌЫЕУїРэгЩЃЎ
ЪБЃЌаЁЭѕЭОжаЪЧЗёашвЊМггЭЃПШєашвЊМггЭЃЌжСЩйашвЊМгЖрЩйЩ§гЭЃПШчВЛашвЊЃЌЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЯТУцЪЧКкАхЩЯГіЪОЕФГпЙцзїЭМЬтЃЌКсЯпЩЯЗћКХДњБэЕФФкШнЃЌе§ШЗЕФЪЧЃЈ ЃЉ
ШчЭМЃЌвбжЊ![]() ЃЌЧѓзїЃК
ЃЌЧѓзїЃК![]() ЃЌЪЙ
ЃЌЪЙ![]() ЃЎ
ЃЎ
зїЗЈЃЛЃЈ1ЃЉвдЕу![]() ЮЊдВаФЃЌ Ђй ЮЊАыОЖЛЛЁЃЌЗжБ№НЛ
ЮЊдВаФЃЌ Ђй ЮЊАыОЖЛЛЁЃЌЗжБ№НЛ![]() гкЕу
гкЕу![]() ЃЛ
ЃЛ
ЃЈ2ЃЉзїЩфЯп![]() ЃЌВЂвдЕу
ЃЌВЂвдЕу![]() ЮЊдВаФЃЌ Ђк ЮЊАыОЖЛЛЁНЛ
ЮЊдВаФЃЌ Ђк ЮЊАыОЖЛЛЁНЛ![]() гкЕу
гкЕу![]() ЃЛ
ЃЛ
ЃЈ3ЃЉвд Ђл ЮЊдВаФЃЌ Ђм ГЄЮЊАыОЖЛЛЁНЛЕкЃЈ2ЃЉВНжаЫљЛЛЁгкЕу![]() ЃЛ
ЃЛ
ЃЈ4ЃЉзїЩфЯп![]() ЃЌ
ЃЌ![]() МДЮЊЫљЧѓзїЕФНЧЃЎ
МДЮЊЫљЧѓзїЕФНЧЃЎ
A.ЂйБэЪО![]() B.ЂкБэЪО
B.ЂкБэЪО![]() C.ЂлБэЪО
C.ЂлБэЪО![]() D.ЂмБэЪОШЮвтГЄ
D.ЂмБэЪОШЮвтГЄ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЮЊБЃГжЫЎЭСЃЌУРЛЏЛЗОГЃЌWжабЇзМБИдкДгаЃУХПкЕНАигЭЙЋТЗЕФетвЛЖЮЭСТЗЕФСНВрддвЛаЉЪїЃЌВЂвЊЧѓЭСТЗСНВрЪїЕФПУЪ§ЯрЕШМфОрвВЯрЕШЃЌЧвЪзЁЂЮВСНЖЫОљддЩЯЪїЃЌЯждкбЇаЃвбБИКУвЛХњЪїУчЃЌШєМфИє30УзддвЛПУЃЌдђШБЩй22ПУЃЛШєМфИє35УзддвЛПУЃЌдђШБЩй14ПУ
ЃЈ1ЃЉЧѓбЇаЃБИКУЕФЪїУчПУЪ§ЃЎ
ЃЈ2ЃЉФГУчЦдИКд№ШЫЬ§ЫЕWжабЇЯыдкаЃЭтЭСТЗСНХдддЪїЕФЩЯЪіЧщПіКѓЃЌОѕЕУСНЪїМфОрЬЋДѓЃЌМШВЛУРЙлЃЌгжгАЯьЗРЗчЙЬЩГЕФаЇЙћЃЌОіЖЈЮоГЅжЇдЎWжабЇ300ПУЪїУчЃЎЧыЮЪЃЌетаЉЪїУчМгЩЯбЇаЃздМКБИКУЕФЪїУчЃЌМфИє5УзддвЛПУЃЌЪЧЗёЙЛгУЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПЙигквЛДЮКЏЪ§y=Љ2x+3ЃЌЯТСаНсТле§ШЗЕФЪЧЃЈЁЁЁЁЃЉ
A. ЭМЯѓЙ§ЕуЃЈ1ЃЌЉ1ЃЉ B. ЭМЯѓОЙ§вЛЁЂЖўЁЂШ§ЯѓЯо
C. yЫцxЕФдіДѓЖјдіДѓ D. ЕБxЃО![]() ЪБЃЌyЃМ0
ЪБЃЌyЃМ0
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПАбвЛИБШ§НЧАхШчЭММзЗХжУЃЌЦфжаЁЯACB=ЁЯDEC=90ЁуЃЌЁЯA=45ЁуЃЌЁЯD=30ЁуЃЌаББпAB=6ЃЌDC=7ЃЌАбШ§НЧАхDCEШЦЕуCЫГЪБеыа§зЊ15ЁуЕУЕНЁїD1CE1ЃЈШчЭМввЃЉЃЌДЫЪБABгыCD1НЛгкЕуOЃЌдђЯпЖЮAD1ЕФГЄЮЊЃЈЁЁЁЁЃЉ
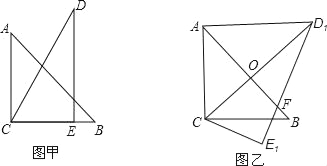
A. ![]() B. 5 C. 4 D.
B. 5 C. 4 D. ![]()
ЁОД№АИЁПB
ЁОНтЮіЁПгЩа§зЊЕФаджЪПЩжЊЃЌдкЭМввжаЃЌЁЯBCE1=15ЁуЃЌЁЯD1CE1=60ЁуЃЌAB=6ЃЌCD1=CD=7ЃЌ
ЁрЁЯD1CB=60Ёу-15Ёу=45ЁуЃЌ
гжЁпЁЯACB=90ЁуЃЌ
ЁрCOЦНЗжЁЯACBЃЌ
гжЁпAC=BCЃЌ
ЁрCOЁЭABЃЌЧвCO=AO=BO=![]() AB=3ЃЌ
AB=3ЃЌ
ЁрD1O=CD1-CO=7-3=4ЃЌЁЯAOD1=90ЁуЃЌ
ЁрдкRtЁїAOD1жаЃЌAD1=![]() .
.
ЙЪбЁB.
ЕуОІЃКБОЬтНтЬтЕФЙиМќЪЧгЩа§зЊЕФаджЪжЄУїЃКЁЯD1CB=45ЁуЃЌДгЖјЕУЕНCD1ЦНЗжЁЯACBЃЌНсКЯЕШбќШ§НЧаЮЕФЁАШ§ЯпКЯвЛЁБжЄЕУЁЯAOD1=90ЁуЃЌВЂЧѓЕУAO=3ЃЌOD1=4ЃЛетбљЮЪЬтОЭБфЕУКмМђЕЅСЫ.
ЁОЬтаЭЁПЕЅбЁЬт
ЁОНсЪјЁП
10
ЁОЬтФПЁПЮвЪаФГаЁЧјЪЕЪЉЙЉХЏИФдьЙЄГЬЃЌЯжМзЁЂввСНЙЄГЬЖгЗжБ№ЭЌЪБПЊЭкСНЬѕ600УзГЄЕФЙмЕРЃЌЫљЭкЙмЕРГЄЖШyЃЈУзЃЉгыЭкОђЪБМфxЃЈЬьЃЉжЎМфЕФЙиЯЕШчЭМЫљЪОЃЌдђЯТСаЫЕЗЈжаЃЌе§ШЗЕФИіЪ§гаЃЈ ЃЉИіЃЎ
ЂйМзЖгУПЬьЭк100УзЃЛ
ЂкввЖгПЊЭкСНЬьКѓЃЌУПЬьЭк50УзЃЛ
ЂлЕБx=4ЪБЃЌМзЁЂввСНЖгЫљЭкЙмЕРГЄЖШЯрЭЌЃЛ
ЂмМзЖгБШввЖгЬсЧА2ЬьЭъГЩШЮЮёЃЎ
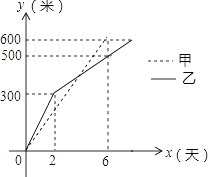
A. 1 B. 2 C. 3 D. 4
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПгУЭЌбљЙцИёЕФКкАзСНжжбеЩЋЕФе§ЗНаЮЃЌАДШчЭМЕФЗНЪНЦДЭМЃЌЧыИљОнЭМжаЕФаХЯЂЭъГЩЯТСаЕФЮЪЬтЃЎ

ЃЈ1ЃЉдкЭМЂкжагУСЫ ПщКкЩЋе§ЗНаЮЃЌдкЭМЂлжагУСЫ ПщКкЩЋе§ЗНаЮЃЛ
ЃЈ2ЃЉАДШчЭМЕФЙцТЩМЬајЦЬЯТШЅЃЌФЧУДЕк![]() ИіЭМаЮвЊгУ ПщКкЩЋе§ЗНаЮЃЛ
ИіЭМаЮвЊгУ ПщКкЩЋе§ЗНаЮЃЛ
ЃЈ3ЃЉШчЙћгазуЙЛЖрЕФАзЩЋе§ЗНаЮЃЌФмВЛФмЧЁКУгУЭъ90ПщКкЩЋе§ЗНаЮЃЌЦДГіОпгавдЩЯЙцТЩЕФЭМаЮЃПШчЙћПЩвдЧыЫЕУїЫќЪЧЕкМИИіЭМаЮЃЛШчЙћВЛФмЃЌЫЕУїФуЕФРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
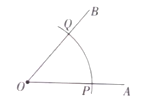
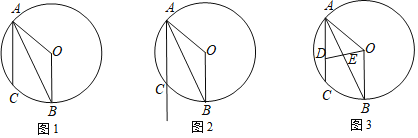
ЁОЬтФПЁПдкдВOжаЃЌAOЁЂBOЪЧдВOЕФАыОЖЃЌЕуCдкСгЛЁ![]() ЩЯЃЌ
ЩЯЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌСЊНсABЃЎ
ЃЌСЊНсABЃЎ
![]() ШчЭМ1ЃЌЧѓжЄЃКABЦНЗж
ШчЭМ1ЃЌЧѓжЄЃКABЦНЗж![]() ЃЛ
ЃЛ
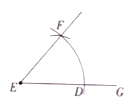
![]() ЕуMдкЯвACЕФбгГЄЯпЩЯЃЌСЊНсBMЃЌШчЙћ
ЕуMдкЯвACЕФбгГЄЯпЩЯЃЌСЊНсBMЃЌШчЙћ![]() ЪЧжБНЧШ§НЧаЮЃЌЧыФудкШчЭМ2жаЛГіЕуMЕФЮЛжУВЂЧѓCMЕФГЄЃЛ
ЪЧжБНЧШ§НЧаЮЃЌЧыФудкШчЭМ2жаЛГіЕуMЕФЮЛжУВЂЧѓCMЕФГЄЃЛ
![]() ШчЭМ3ЃЌЕуDдкЯвACЩЯЃЌгыЕуAВЛжиКЯЃЌСЊНсODгыЯвABНЛгкЕуEЃЌЩшЕуDгыЕуCЕФОрРыЮЊxЃЌ
ШчЭМ3ЃЌЕуDдкЯвACЩЯЃЌгыЕуAВЛжиКЯЃЌСЊНсODгыЯвABНЛгкЕуEЃЌЩшЕуDгыЕуCЕФОрРыЮЊxЃЌ![]() ЕФУцЛ§ЮЊyЃЌЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ЕФУцЛ§ЮЊyЃЌЧѓyгыxЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com