
【题目】已如两个全等的等腰△ABC、△DEF,其中∠ACB=∠DFE=90°,E为AB中点,△DEF可绕顶点E旋转,线段DE,EF分别交线段CA,CB(或它们所在的直线)于M、N.
(1)如图1,当线段EF经过△ABC的顶点时,点N与点C重合,线段DE交AC于M,已知AC=BC=5,则MC= ;
(2)如果2,当线段EF与线段BC边交于N点,线段DE与线段AC交于M点,连MN,EC,请探究AM,MN,CN之间的等量关系,并说明理由;
(3)如图3,当线段EF与BC延长线交于N点,线段DE与线段AC交于M点,连MN,EC,则(2)中AM,MN,CN之间的等量关系还成立吗?请说明理由.

【答案】(1)![]() ;(2)见解析;(3)见解析
;(2)见解析;(3)见解析
【解析】
(1)根据AC=BC,E为AB中点,得出CE⊥AB,∠ACE=∠BCE=![]() ∠ACB=45°,∠A=∠ACE=45°,AE=CE,再根据DF=EF,∠DFE=90°,得出∠FED=45°,∠FED=
∠ACB=45°,∠A=∠ACE=45°,AE=CE,再根据DF=EF,∠DFE=90°,得出∠FED=45°,∠FED=![]() ∠AEC,即可得出AM=MC;
∠AEC,即可得出AM=MC;
(2)先在AM截取AH,使得AH=CN,连接EH,根据AE=CE,∠A=∠BCE=45°证出△AHE≌△CNE,HE=NE,∠AEH=∠CEN,∠HEM=∠AEC﹣∠AEH﹣MEC=∠AEC﹣∠CEN﹣MEC=∠AEC﹣∠MEF=90°﹣45°=45°,∠HEM=∠NEM=45°然后证出△HEM≌△NEM,HM=MN,最后根据AM=AH+HM=CN+MN即可得出答案;
(3)先在CB上截取CH=AM,根据SAS证得△AEM≌△CEH,得出EM=EH,∠AEM=∠CEH,AM=CH,再根据∠MEN和∠AEC的度数,得出∠CEH+∠CEN=∠HEN=45°,再在△EMN和△EHN中,根据SAS证得△EMN≌△EHN,得出MN=HN,即可求出答案.
解:(1)∵AC=BC,E为AB中点,
∴CE⊥AB,∠ACE=∠BCE=![]() ∠ACB=45°,
∠ACB=45°,
∴∠A=∠ACE=45°,
∴∠AEC=90°,AE=CE,
∵DF=EF,∠DFE=90°,
∴∠FED=45°,
∴∠FED=![]() ∠AEC,
∠AEC,
又∵AE=CE,
∴AM=MC=![]() AC=
AC=![]() ,
,
故答案为:![]() ;
;
(2)AM=MN+CN,理由如下:
如图2,在AM截取AH,使得AH=CN,连接EH,
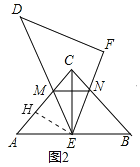
由(1)知AE=CE,∠A=∠BCE=45°
∵在△AHE与△CNE中:
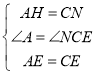 ,
,
∴△AHE≌△CNE(SAS),
∴HE=NE,∠AEH=∠CEN,
∴∠HEM=∠AEC﹣∠AEH﹣MEC=∠AEC﹣∠CEN﹣MEC=∠AEC﹣∠MEF=90°﹣45°=45°,
∴∠HEM=∠NEM=45
∵在△HEM与△NEM中:
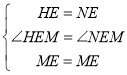 ,
,
∴△HEM≌△NEM(SAS),
∴HM=MN,
∴AM=AH+HM=CN+MN,
即AM=MN+CN;
(3)猜得:MN=AM+CN,理由如下:
如图3,在CB上截取CH=AM,连接EH,
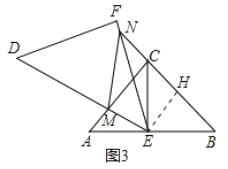
在△AEM和△CEH中,
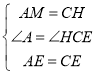 ,
,
∴△AEM≌△CEH(SAS),
∴EM=EH,∠AEM=∠CEH,AM=CH,
∵∠MEN=45°,∠AEC=90°,
∴∠AEM+∠CEN=45°,
∴∠CEH+∠CEN=∠HEN=45°,
∵∠MEN=∠HEN,
在△EMN和△EHN中,
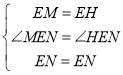 ,
,
∴△EMN≌△EHN(SAS),
∴MN=HN,
∴MN=CH+CN,
∴MN=AM+CN.


科目:初中数学 来源: 题型:
【题目】已知![]() 是
是![]() 的平分线,点
的平分线,点![]() 是射线
是射线![]() 上一点,点C、D分别在射线
上一点,点C、D分别在射线![]() 、
、![]() 上,连接PC、PD.
上,连接PC、PD.
(1)发现问题
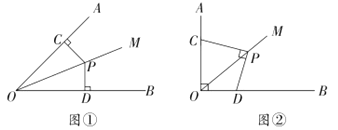
如图①,当![]() ,
,![]() 时,则PC与PD的数量关系是________.
时,则PC与PD的数量关系是________.
(2)探究问题
如图②,点C、D在射线OA、OB上滑动,且∠AOB=90°,∠OCP+∠ODP=180°,当![]() 时,PC与PD在(1)中的数量关系还成立吗?说明理由.
时,PC与PD在(1)中的数量关系还成立吗?说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置.此时AC′的中点恰好与点D重合,AB′交CD于点E,若AB=3,则△AEC的面积为( )
A.3
B.![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10.
(Ⅰ)如图①,在OA上取一点E,将△EOC沿EC折叠,使点O落在AB边上的D点,求E点的坐标;
(Ⅱ)如图②,在OA、OC边上选取适当的点E′、F,将△E′OF沿E′F折叠,使O点落在AB边上D′点,过D′作D′G∥OA交E′F于T点,交OC于G点,设T的坐标为(x,y),求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若OG=2 ![]() ,求△D′TF的面积.(直接写出结果即可)
,求△D′TF的面积.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )

A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形 ACDE 是证明勾股定理时用到的一个图形,a 、b 、c 是 RtABC和 RtBED 的边长,已知![]() ,这时我们把关于 x 的形如
,这时我们把关于 x 的形如![]() 二次方程称为“勾系一元二次方程”.
二次方程称为“勾系一元二次方程”.

请解决下列问题:
(1)写出一个“勾系一元二次方程”;
(2)求证:关于 x 的“勾系一元二次方程”![]() ,必有实数根;
,必有实数根;
(3)若 x 1是“勾系一元二次方程” ![]() 的一个根,且四边形 ACDE 的周长是6
的一个根,且四边形 ACDE 的周长是6![]() ,求ABC 的面积.
,求ABC 的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日天气晴朗,某集团公司准备组织全体员工外出踏青.决定租用甲、乙、丙三种型号的巴士出行,甲型巴士每辆车的乘载量是乙型巴士的3倍,丙型巴士每辆可乘坐36人.现在旅游公司有甲、乙、丙型巴士若干辆,预计给该集团公司安排申型、丙型巴士共计8辆,其余员工安排乙型巴士,每辆巴士均满载,这样乘坐乙型巴士和丙型巴士的员工共296人.临行前,突然有若干人因特殊原因请假,这样一来刚好可以减少租用一辆乙型包士,且有一辆乙型巴士多出两个空位,这样甲、乙两种型号巴士共计装载178人;则该集团公司共有________名员工.
查看答案和解析>>
科目:初中数学 来源: 题型:
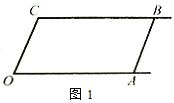
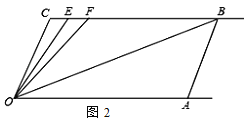
【题目】如图1,已知射线CB∥OA,∠C=∠OAB,
(1)求证:AB∥OC;
(2)如图2,E、F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
①当∠C=110°时,求∠EOB的度数.
②若平行移动AB,那么∠OBC :∠OFC的值是否随之发生变化?若变化,找出变
化规律;若不变,求出这个比值.
查看答案和解析>>
科目:初中数学 来源: 题型:
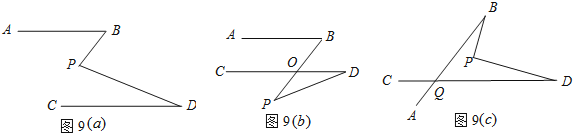
【题目】如图,平面内的直线有相交和平行两种位置关系.
(1)如图(a),已知AB∥CD,求证:∠BPD=∠B+∠D.
(2)如图(b),已知AB∥CD,求证:∠BOD=∠P+∠D.
(3)根据图(c),试判断∠BPD,∠B,∠D,∠BQD之间的数量关系,并说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com