
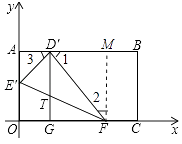
【题目】将一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10.
(Ⅰ)如图①,在OA上取一点E,将△EOC沿EC折叠,使点O落在AB边上的D点,求E点的坐标;
(Ⅱ)如图②,在OA、OC边上选取适当的点E′、F,将△E′OF沿E′F折叠,使O点落在AB边上D′点,过D′作D′G∥OA交E′F于T点,交OC于G点,设T的坐标为(x,y),求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若OG=2 ![]() ,求△D′TF的面积.(直接写出结果即可)
,求△D′TF的面积.(直接写出结果即可)
【答案】解:(Ⅰ)∵将△EOC沿EC折叠,使O点落在AB边上的D点,
∴DC=OC=10.
在Rt△BCD中,∵∠B=90°,BC=OA=6,DC=10,
∴BD= ![]() =8.
=8.
在Rt△AED中,∵∠DAE=90°,AD=2,DE=OE,AE=6﹣OE,
∴DE2=AD2+AE2,即OE2=22+(6﹣OE)2,
解得 OE= ![]() ,
,
∴E点的坐标为(0, ![]() );
);
(Ⅱ)∵将△E′OF沿E′F折叠,使O点落在AB边上D′点,
∴∠D′E′F=∠OE′F,D′E′=OE′,
∵D′G∥AO,
∴∠OE′F=∠D′TE′,
∴∠D′E′F=∠D′TE′,
∴D′T=D′E′=OE′,
∴TG=AE′;
∵T(x,y),
∴AD′=x,TG=AE′=y,D′T=D′E′=OE′=6﹣y.
在Rt△AD′E′中,∵∠D′AE′=90°,
∴AD′2+AE′2=D′E′2,即x2+y2=(6﹣y)2,
整理,得y=﹣ ![]() x2+3;
x2+3;
由(1)可得AD′=OG=2时,x最小,从而x≥2,
当E′F恰好平分∠OAB时,AD′最大即x最大,
此时G点与F点重合,四边形AOFD′为正方形,即x最大为6,从而x≤6,
故变量x的取值范围是2≤x≤6.
(Ⅲ)∵T的坐标为(x,y),y=﹣ ![]() x2+3,OG=2
x2+3,OG=2 ![]() ,
,
∴GT=y=﹣ ![]() ×12+3=2,AD'=OG=2
×12+3=2,AD'=OG=2 ![]() ,
,
∴DT=6﹣2=4,
作FM⊥AB于M,则FM=BC=6,∠FMD'=90°=∠A,
∴∠1+∠2=90°,
由折叠的性质得:∠ED'F=∠AOC=90°,
∴∠1+∠3=90°,
∴∠2=∠3,
∴△D'MF∽△EAD',
∴ ![]() =
= ![]() ,即
,即 ![]() =
= ![]() =
= ![]() ,
,
设E'O=ED'=x,则AE'=6﹣x,
在Rt△AD'E'中,由勾股定理得:(2 ![]() )2+(6﹣x)2=x2,
)2+(6﹣x)2=x2,
解得:x=4,
∴OF=D'F=4 ![]() ,
,
∴GF=OF﹣OG=2 ![]() ,
,
∴△D′TF的面积= ![]() D'TGF=
D'TGF= ![]() ×4×2
×4×2 ![]() =4
=4 ![]() .
.
【解析】(1)利用折叠性质和勾股定理,构建方程,即可求出E坐标;(2)利用折叠的性质、勾股定理构建方程,变形为函数解析式形式即可;(3)由折叠可得相似三角形,对应边成比例可求出E'O,进一步求出面积.
【考点精析】根据题目的已知条件,利用翻折变换(折叠问题)和相似三角形的判定与性质的相关知识可以得到问题的答案,需要掌握折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等;相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.


科目:初中数学 来源: 题型:
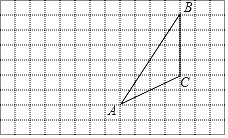
【题目】画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.
(1)将△ABC向左平移4格,再向下平移1格,请在图中画出平移后的△A'B'C';
(2)利用网格线在图中画出△ABC的中线CD,高线AE;
(3)△A'B'C'的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B分别在函数y=![]() (k1>0)与函数y=
(k1>0)与函数y=![]() (k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )
(k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )

A.2B.4C.6D.8
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a、b、c为常数,且a≠0)中x与y的部分对应值如表:
x | ﹣1 | 0 | 1 | 3 |
y | ﹣1 | 3 | 5 | 3 |
①ac<0;
②当x>1时,y的值随x值的增大而减小;
③x=3是方程ax2+(b﹣1)x+c=0的一个根;
④当﹣1<x<3时,ax2+(b﹣1)x+c>0.
上述结论中正确的个数是( )
A.4
B.3
C.2
D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连接BC.
(Ⅰ)如图①,若∠P=20°,求∠BCO的度数;
(Ⅱ)如图②,过A作弦AD⊥OP于E,连接DC,若OE= ![]() CD,求∠P的度数.
CD,求∠P的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点O为对角线AC的中点,过点o作射线OG、ON分别交AB,BC于点E,F,且∠EOF=90°,BO、EF交于点P.则下列结论中:
⑴图形中全等的三角形只有两对;
⑵正方形ABCD的面积等于四边形OEBF面积的4倍;
⑶BE+BF= ![]() OA;
OA;
⑷AE2+CF2=2OPOB.
正确的结论有( )个.
A.1
B.2
C.3
D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已如两个全等的等腰△ABC、△DEF,其中∠ACB=∠DFE=90°,E为AB中点,△DEF可绕顶点E旋转,线段DE,EF分别交线段CA,CB(或它们所在的直线)于M、N.
(1)如图1,当线段EF经过△ABC的顶点时,点N与点C重合,线段DE交AC于M,已知AC=BC=5,则MC= ;
(2)如果2,当线段EF与线段BC边交于N点,线段DE与线段AC交于M点,连MN,EC,请探究AM,MN,CN之间的等量关系,并说明理由;
(3)如图3,当线段EF与BC延长线交于N点,线段DE与线段AC交于M点,连MN,EC,则(2)中AM,MN,CN之间的等量关系还成立吗?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
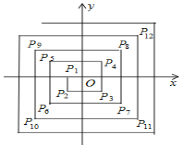
【题目】如图,在平面直角坐标系中,从点P1(﹣1,0),P2(﹣1,﹣1),P3(1,﹣1),P4(1,1),P5(﹣2,1),P6(﹣2,﹣2),…依次扩展下去,则P2020的坐标为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
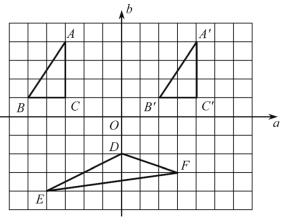
【题目】在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,回答下列问题.
(1)图中格点三角形A′B′C′是由格点三角形ABC通过怎样的变换得到的?
(2)如果以直线a,b为坐标轴建立平面直角坐标系后,点A的坐标为(-3,4),请求出三角形DEF的面积S.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com