练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

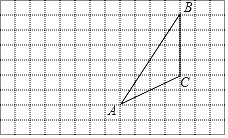
    【题目】画图并填空：如图，每个小正方形的边长为1个单位，每个小正方形的顶点叫格点．

    (1)将△ABC向左平移4格，再向下平移1格，请在图中画出平移后的△A'B'C'；

    (2)利用网格线在图中画出△ABC的中线CD，高线AE；

    (3)△A'B'C'的面积为　 　．

    【答案】(1)见解析；(2)见解析；(3)8

    【解析】

    (1)根据平移的性质即可将△ABC向左平移4格，再向下平移1格，进而画出平移后的△A'B'C'；

    (2)利用网格线即可在图中画出△ABC的中线CD，高线AE；

    (3)根据网格得出底盒高，然后根据三角形面积公式即可求出△A'B'C'的面积．

    解：(1)如图，△A'B'C'即为所求；

    (2)如图，中线CD，高线AE即为所求；

    (3)△ABC的面积为：，

    ∵△A'B'C'是由△ABC平移得到，

    ∴△A'B'C'的面积=△ABC的面积=8，

    故答案为：8．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某校为了开展“阳光体育运动”，计划购买篮球、足球共60个，已知每个篮球的价格为70元，每个足球的价格为80元.

    （1）若购买这两类球的总金额为4600元，求篮球、足球各买了多少个？

    （2）若购买篮球的总金额不超过购买足球的总金额，求最多可购买多少个篮球？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】问题提出

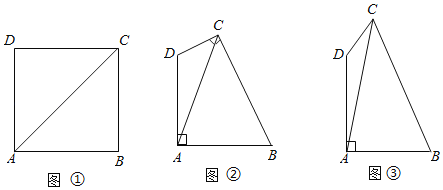
    (1)如图①，在正方形ABCD中，对角线AC=8，则正方形ABCD的面积为　 　；

    问题探究

    (2)如图②，在四边形ABCD中，AD=AB，∠DAB=∠DCB=90°，∠ADC+∠ABC=180°，若四边形ABCD的面积为8，求对角线AC的长；

    问题解决

    (3)如图③，四边形ABCD是张叔叔要准备开发的菜地示意图，其中边AD和AB是准备用砖来砌的砖墙，且满足AD=AB，∠DAB=90°，边DC和CB是准备用现有的长度分别为3米和7米的竹篱笆来围成的篱笆墙，即DC=3米，CB=7米．按照这样的想法，张叔叔围成的菜园里对角线AC的长是否存在最大值呢？若存在，求出这个最大值；若不存在，说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图（1），E是直线AB、CD内部一点，AB∥CD，连接EA、ED．

    （1）探究：

    ①若∠A=30°，∠D=40°，则∠AED等于多少度？

    ②若∠A=20°，∠D=60°，则∠AED等于多少度？

    ③在图（1）中∠AED、∠EAB、∠EDC有什么数量关系，并证明你的结论．

    （2）拓展：如图（2），射线FE与矩形ABCD的边AB交于点E，与边CD交于点F，①②③④分别是被射线FE隔开的四个区域（不含边界，其中③④位于直线AB的上方），P是位于以上四个区域上点，猜想：∠PEB、∠PFC、∠EPF之间的关系．（不要求证明）

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，抛物线 y=ax2+bx+c 与 x 轴交于A（1,0），B（-3,0），与 y 轴交于C（0，3），顶点是G.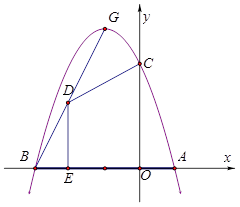
    （1）求抛物线的的解析式及顶点坐标G.
    （2）如图1，点D（x，y）是线段BG上的动点（不与B，G重合），DE⊥x轴于E，设四边形OEDC的面积为S，求S与x之间的函数关系式，并求S的最大值.
    （3）如图2，将抛物线 y=ax2+bx+c 向下平移 k 个单位，平移后的顶点式 G' ，与 x 轴的交点是 A'，B' .若△A'B'G' 是直角三角形，求 k 的值.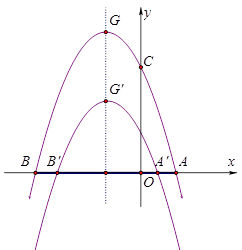

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，的位置如图所示．

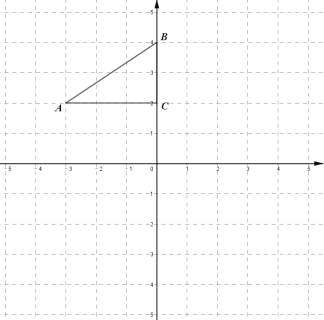
    （1）画出先向右平移3个单位，再向下平移6个单位后得到的，并写出，各顶点的坐标；

    （2）画出绕点逆时针旋转后得到的，并写出，各顶点的坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】已知是的平分线，点是射线上一点，点C、D分别在射线、上，连接PC、PD．

    （1）发现问题

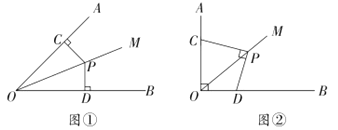
    如图①，当，时，则PC与PD的数量关系是________．

    （2）探究问题

    如图②，点C、D在射线OA、OB上滑动，且∠AOB=90°，∠OCP＋∠ODP=180°，当时，PC与PD在（1）中的数量关系还成立吗？说明理由．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

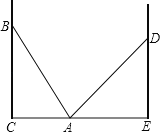
    【题目】如图，在两面墙之间有一个底端在A点的梯子，当它靠在一侧的墙上时，梯子的顶端在B点，当它靠在另一侧的墙上时，梯子的顶端在D点，已知∠BAC＝60°，点B到地面的垂直距离BC＝5米，DE＝6米．

    （1）求梯子的长度；

    （2）求两面墙之间的距离CE．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】将一矩形纸片OABC放在直角坐标系中，O为原点，C在x轴上，OA=6，OC=10．
    （Ⅰ）如图①，在OA上取一点E，将△EOC沿EC折叠，使点O落在AB边上的D点，求E点的坐标；
    （Ⅱ）如图②，在OA、OC边上选取适当的点E′、F，将△E′OF沿E′F折叠，使O点落在AB边上D′点，过D′作D′G∥OA交E′F于T点，交OC于G点，设T的坐标为（x，y），求y与x之间的函数关系式，并直接写出自变量x的取值范围；
    （Ⅲ）在（Ⅱ）的条件下，若OG=2 ，求△D′TF的面积．（直接写出结果即可）

    查看答案和解析>>

    同步练习册答案