
【题目】问题提出
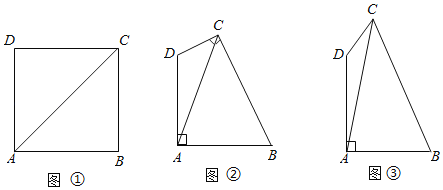
(1)如图①,在正方形ABCD中,对角线AC=8,则正方形ABCD的面积为 ;
问题探究
(2)如图②,在四边形ABCD中,AD=AB,∠DAB=∠DCB=90°,∠ADC+∠ABC=180°,若四边形ABCD的面积为8,求对角线AC的长;
问题解决
(3)如图③,四边形ABCD是张叔叔要准备开发的菜地示意图,其中边AD和AB是准备用砖来砌的砖墙,且满足AD=AB,∠DAB=90°,边DC和CB是准备用现有的长度分别为3米和7米的竹篱笆来围成的篱笆墙,即DC=3米,CB=7米.按照这样的想法,张叔叔围成的菜园里对角线AC的长是否存在最大值呢?若存在,求出这个最大值;若不存在,说明理由.
【答案】(1)32;(2)4;(3)存在,最大值为5![]() .
.
【解析】
(1)先根据勾股定理求出AB的长,然后再根据面积公式解答即可;
(2)先说明△ADC'≌△ABC(SAS),进而得出S△ADC'=S△ABC,AC'=AC,然后再根据面积公式解答即可;
(3先判断出点D在CC'上时, AC最大,求出AC的长即可.
解:(1)∵AC是正方形的对角线,
∴∠B=90°,AB=BC,
在Rt△ABC中,AC=8,
根据勾股定理得,AB2+BC2=AC2,
∴2AB2=AC2=64,
∴AB2=32,
∴S正方形ABCD=32,
故答案为32;
(2)如图②,延长CD至C'使DC'=BC,连接AC',
∴∠ADC+∠ADC'=180°,
∵∠ADC+∠ABC=180°,
∴∠ADC'=∠ABC,
∵AD=AB,
∴△ADC'≌△ABC(SAS),
∴S△ADC′=S△ABC,AC'=AC,
∴∠DAC'=∠BAC,
∴∠DAC'+∠CAD=∠BAC+∠CAD=∠BAD=90°,
∴∠CAC'=90°,
∵S四边形ABCD=S△ABC+S△ADC=S△ADC′+S△ADC=S△ACC′=8,
∵S△ACC′=![]() ACAC'=
ACAC'=![]() AC2=8,
AC2=8,
∴AC=4,
即AC的长为4;
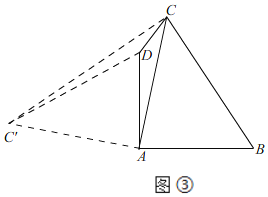
(3)如图③,
将△ABC绕点A逆时针旋转90°得△ADC',连接AC',CC',
由旋转知,AC'=AC,C'D=BC,∠CAC'=90°,
当点D在CC'上时,AC最大
此时,CC'=CD+C'D=CD+BC=10,
∴AC2=![]() CC'2=50,
CC'2=50,
∴AC=5![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,二次函数y=ax2+bx+c的图象开口向上,对称轴为直线x=1,图象经过(3,0).下列结论中,正确的一项是( )
A.![]() <0
<0
B.![]() <0
<0
C.![]() <0
<0
D.![]() 4acb2
4acb2![]() 0
0
查看答案和解析>>
科目:初中数学 来源: 题型:
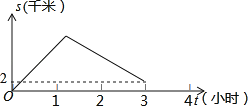
【题目】重庆某著名景区依托天然河道新开发了一款乘船体验项目.小明乘船由甲地顺流而下到乙地,然后由乙地逆流而上到丙地,然后靠岸乘车离开景点.若水流速度为2km/小时,船在静水中的速度为8km/小时.在整个乘船过程中,轮船与甲地相距的路程S(千米)与轮船出发的时间t(小时)之间的关系如图所示,甲乙两地间的距离为_____千米.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)计算:﹣12+(π﹣3.14)0﹣(﹣![]() )﹣2+
)﹣2+![]() ;
;
(2)先化简,再求值:[(2x+y)(2x﹣y)+(x+y)2﹣2(2x2﹣xy)]÷(﹣![]() x),其中x、y满足
x),其中x、y满足![]() +(y+4)2=0.
+(y+4)2=0.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校为庆祝国庆节举办游园活动,小军来到摸球兑奖活动场地,李老师对小军说:“这里有甲、乙两个盒子,里面都装有一些乒乓球,你只能选择在其中一个盒子中摸球。”获奖规则如下:
甲盒中有白色乒乓球4个,黄色乒乓球1个,一人只能摸一次且一次摸出一个球,若这个球为黄色球,则可获得玩具熊一个,否则不得奖;
乙盒中有白色乒乓球2个,黄色乒乓球3个,一人只能摸一次且一次摸出两个球,若这两个球均为黄色球,则可获得玩具熊一个,否则不得奖;
请问小军在哪个盒子内摸球获得玩具熊的机会更大?请用概率知识说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
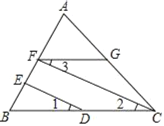
【题目】请你完成下面的证明:
已知:如图,∠GFB+∠B=180°,∠1=∠3,
求证:FC∥ED.
证明:∵∠GFB+∠B=180°
∴FG∥BC( )
∴∠3= ( ),
又∵∠1=∠3(已知)
∴∠1= (等量代换)
∴FC∥ED( )
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将一把两边都带有刻度的直尺放在半圆形纸片上,使其一边经过圆心O,另一边所在直线与半圆相交于点D、E,量出半径OC=5cm,弦DE=8cm,求直尺的宽度.
查看答案和解析>>
科目:初中数学 来源: 题型:
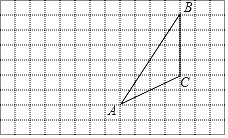
【题目】画图并填空:如图,每个小正方形的边长为1个单位,每个小正方形的顶点叫格点.
(1)将△ABC向左平移4格,再向下平移1格,请在图中画出平移后的△A'B'C';
(2)利用网格线在图中画出△ABC的中线CD,高线AE;
(3)△A'B'C'的面积为 .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点A,B分别在函数y=![]() (k1>0)与函数y=
(k1>0)与函数y=![]() (k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )
(k2<0)的图象上,线段AB的中点M在x轴上,△AOB的面积为4,则k1﹣k2的值为( )

A.2B.4C.6D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com