
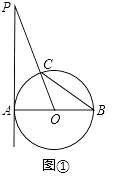
【题目】如图,AB是⊙O的直径,PA切⊙O于A,OP交⊙O于C,连接BC.
(Ⅰ)如图①,若∠P=20°,求∠BCO的度数;
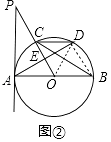
(Ⅱ)如图②,过A作弦AD⊥OP于E,连接DC,若OE= ![]() CD,求∠P的度数.
CD,求∠P的度数.
【答案】解:(Ⅰ)如图1中,
∵PA是⊙O的切线,
∴OA⊥AP,
∴∠PAO=90°,∵∠P=20°,
∴∠AOC=90°﹣20°=70°,
∴∠B= ![]() ∠AOC=35°,
∠AOC=35°,
∵OB=OC,
∴∠B=∠OCB=35°,
∴∠BCO=35°.
(Ⅱ)如图2中,连接BD、OD.
∵AD⊥OP于E,
∴AE=ED, ![]() =
= ![]() ,
,
∵AE=ED,OA=OB,
∴OE= ![]() DB,
DB,
∵OE= ![]() CD,
CD,
∴CD=DB,
∴ ![]() =
= ![]() ,
,
∴ ![]() =
= ![]() =
= ![]() ,
,
∴∠AOC=∠COD=∠BOD=60°,
∵PA是⊙O的切线,
∴∠PAO=90°,
∴∠P=30°
【解析】(1)可利用切线的性质得出垂直,再利用等边对等角的性质求出答案;(2)可利用直径的性质须连接BD,构成90度的圆周角,再利用垂径定理及其推论可求出∠P=30°.
【考点精析】解答此题的关键在于理解垂径定理的相关知识,掌握垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧,以及对切线的性质定理的理解,了解切线的性质:1、经过切点垂直于这条半径的直线是圆的切线2、经过切点垂直于切线的直线必经过圆心3、圆的切线垂直于经过切点的半径.


科目:初中数学 来源: 题型:
【题目】如图1,抛物线 y=ax2+bx+c 与 x 轴交于A(1,0),B(-3,0),与 y 轴交于C(0,3),顶点是G.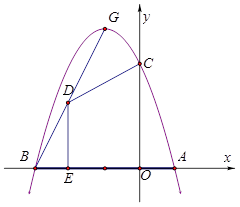
(1)求抛物线的的解析式及顶点坐标G.
(2)如图1,点D(x,y)是线段BG上的动点(不与B,G重合),DE⊥x轴于E,设四边形OEDC的面积为S,求S与x之间的函数关系式,并求S的最大值.
(3)如图2,将抛物线 y=ax2+bx+c 向下平移 k 个单位,平移后的顶点式 G' ,与 x 轴的交点是 A',B' .若△A'B'G' 是直角三角形,求 k 的值.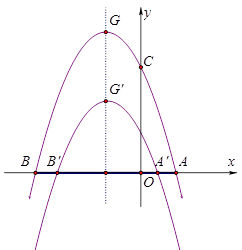
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为加快5G网络建设,某移动通信公司在山顶上建了一座5G信号通信塔AB,山高BE=100米(A,B,E在同一直线上),点C与点D分别在E的两侧(C,E,D在同一直线上),BE⊥CD,CD之间的距离1000米,点D处测得通信塔顶A的仰角是30°,点C处测得通信塔顶A的仰角是45°(如图),则通信塔AB的高度约为( )米.(参考数据:![]() ,
,![]() )
)

A.350B.250C.200D.150
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD绕点A旋转至矩形AB′C′D′位置.此时AC′的中点恰好与点D重合,AB′交CD于点E,若AB=3,则△AEC的面积为( )
A.3
B.![]()
C.2 ![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】重庆不仅是网红城市,更是拥有长安,力帆等大型车企的一座汽车城,为了更好的推广和销售汽车,每年都会在悦来会展中心举办大型车展.去年该车展期间大众旗下两品牌汽车迈腾和途观L共计销售240辆,迈腾销售均价为每辆20万元,途观L销售均价为每辆30万元,两种车型去年车展期间销售额共计5600万元.
(1)这两种车型在去年车展期间各销售了多少辆?
(2)在今年的该车展上,各大汽车经销商纷纷采取降价促销手段,而途观L坚持不降价,与去年相比,销售均价不变,销量比去年车展期间减少了a%,而迈腾销售均价比去年降低了a%,销量较去年增加了2a%,两种车型今年车展期间销售总额与去年相同,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一矩形纸片OABC放在直角坐标系中,O为原点,C在x轴上,OA=6,OC=10.
(Ⅰ)如图①,在OA上取一点E,将△EOC沿EC折叠,使点O落在AB边上的D点,求E点的坐标;
(Ⅱ)如图②,在OA、OC边上选取适当的点E′、F,将△E′OF沿E′F折叠,使O点落在AB边上D′点,过D′作D′G∥OA交E′F于T点,交OC于G点,设T的坐标为(x,y),求y与x之间的函数关系式,并直接写出自变量x的取值范围;
(Ⅲ)在(Ⅱ)的条件下,若OG=2 ![]() ,求△D′TF的面积.(直接写出结果即可)
,求△D′TF的面积.(直接写出结果即可)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC 中,AB=3,AC=4,BC=5,P 为边 BC 上一动点,PE⊥AB 于 E,PF⊥AC于 F,M 为 EF 中点,则 AM 的最小值为( )

A.1B.1.3C.1.2D.1.5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】近日天气晴朗,某集团公司准备组织全体员工外出踏青.决定租用甲、乙、丙三种型号的巴士出行,甲型巴士每辆车的乘载量是乙型巴士的3倍,丙型巴士每辆可乘坐36人.现在旅游公司有甲、乙、丙型巴士若干辆,预计给该集团公司安排申型、丙型巴士共计8辆,其余员工安排乙型巴士,每辆巴士均满载,这样乘坐乙型巴士和丙型巴士的员工共296人.临行前,突然有若干人因特殊原因请假,这样一来刚好可以减少租用一辆乙型包士,且有一辆乙型巴士多出两个空位,这样甲、乙两种型号巴士共计装载178人;则该集团公司共有________名员工.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC,AB=AC,以AB为直径的⊙O分别交AC,BC于点D,E,点F在AC的延长线上,且∠CBF= ![]() ∠CAB.
∠CAB.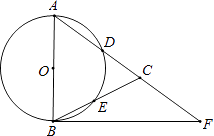
(1)求证:直线BF是⊙O的切线;
(2)若AB=5,sin∠CBF= ![]() ,求BC和BF的长.
,求BC和BF的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com