
【题目】如图,将一张直角三角形ABC纸片沿斜边AB上的中线CD剪开,得到△ACD,再将△ACD沿DB方向平移到△A′C′D′的位置,若平移开始后点D′未到达点B时,A′C′交CD于E,D′C′交CB于点F,连接EF,当四边形EDD′F为菱形时,试探究△A′DE的形状,并判断△A′DE与△EFC′是否全等?请说明理由.
【答案】解:当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.
理由:∵△BCA是直角三角形,∠ACB=90°,AD=DB,
∴CD=DA=DB,
∴∠DAC=∠DCA,
∵A′C∥AC,
∴∠DA′E=∠A,∠DEA′=∠DCA,
∴∠DA′E=∠DEA′,
∴DA′=DE,
∴△A′DE是等腰三角形.
∵四边形DEFD′是菱形,
∴EF=DE=DA′,EF∥DD′,
∴∠CEF=∠DA′E,∠EFC=∠CD′A′,
∵CD∥C′D′,
∴∠A′DE=∠A′D′C=∠EFC,
在△A′DE和△EFC′中, ,
,
∴△A′DE≌△EFC′.
【解析】当四边形EDD′F为菱形时,△A′DE是等腰三角形,△A′DE≌△EFC′.先证明CD=DA=DB,得到∠DAC=∠DCA,由AC∥A′C′即可得到∠DA′E=∠DEA′由此即可判断△DA′E的形状.由EF∥AB推出∠CEF=∠EA′D,∠EFC=∠A′D′C=∠A′DE,再根据A′D=DE=EF即可证明.


 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图,直线y=-3x与双曲线y=![]() 在第四象限内的部分相交于点A(a,-6),将这条直线向
在第四象限内的部分相交于点A(a,-6),将这条直线向
上平移后与该双曲线交于点M,且△AOM的面积为3.
(1)求k的值;
(2)求平移后得到的直线的函数表达式.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在下列条件中,不能证明△ABD≌△ACD的是( ).
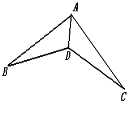
A.BD=DC, AB=AC B.∠ADB=∠ADC,BD=DC
C.∠B=∠C,∠BAD=∠CAD D. ∠B=∠C,BD=DC
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】 如图,△ABC中,AB=AC,∠BAC=90°,点D是直线AB上的一动点(不和A、B重合),BE⊥CD于E,交直线AC于F.
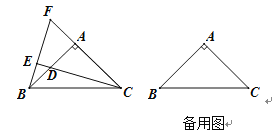
(1)点D在边AB上时,试探究线段BD、AB和AF的数量关系,并证明你的结论;
(2)点D在AB的延长线或反向延长线上时,(1)中的结论是否成立?若不成立,请直接写出正确结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠BAC=90°,AB=AC,AD⊥BC于D,AE平分∠BAD,交BC于E,在△ABC外有一点F,使FA⊥AE,FC⊥BC.
(1)求证:BE=CF;
(2)在AB上取一点M,使得BM=2DE,连接ME
①求证:ME⊥BC;
②求∠EMC的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC和△DBE中,BC=BE,还需再添加两个条件才能使△ABC≌△DBE,则不能添加的一组条件是( )

A. AB=DB,∠ A=∠ D B. DB=AB,AC=DE C. AC=DE,∠C=∠E D. ∠ C=∠ E,∠ A=∠ D
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC与△DEF分别是等边三角形和等腰直角三角形,AC与DF交于点G,AD与FC分别是△ABC和△DEF的高,线段BC,DE在同一条直线上,则下列说法不正确的是( ) 
A.△AGD∽△CGF
B.△AGD∽△DGC
C.![]() =3
=3
D.![]() =
= ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知在△ABC中,∠BAC=90°,过点C的直线EF∥AB,D是BC上一点,连接AD,过点D分别作GD⊥AD,HD⊥BC,交EF和AC于点G,H,连接AG.
(1)当∠ACB=30°时,如图1所示.
①求证:△GCD∽△AHD;
②试判断AD与DG之间的数量关系,并说明理由;
(2)当tan∠ACB= ![]() 时,如图2所示,请你直接写出AD与DG之间的数量关系.
时,如图2所示,请你直接写出AD与DG之间的数量关系.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com