
����Ŀ���������������a��b��cΪһ�鹴��������ô4a��4b��4c���ǹ�����������������ε������ڽǵĶ�������3��4��5����ô�����������ֱ�������Σ������һ�������ε�������12��25��21����ô�������α���ֱ�������Σ���һ������ֱ�������ε�������a��b��c����a��b��c������ôa2��b2��c2��2��1��1��������ȷ���ǣ�������
A.�٢�B.�٢�C.�٢�D.�ڢ�
���𰸡�C
��������
�ֱ����ù������Ķ��塢���ɶ����Լ�����ֱ�������εıߵĹ�ϵ�ֱ��жϵó����ɣ�
�⣺�����a��b��cΪһ�鹴��������ô4a��4b��4c���ǹ��������������⣻
����������ε������ڽǵĶ�������3��4��5�����������ε������ڽǶ���Ϊ��45�㣬60��,75�㣬�����������β���ֱ�������Σ�ԭ�����Ǽ����⣻
�����һ�������ε�������12��25��21����Ϊ![]() ���ʴ������β���ֱ�������Σ���ԭ�����Ǽ����⣻
���ʴ������β���ֱ�������Σ���ԭ�����Ǽ����⣻
��һ������ֱ�������ε�������a��b��c����a��b��c������ôa2��b2��c2��2��1��1���������⣻
��ѡ��C��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��x+3��x�ύ�ڵ�B����y�ύ�ڵ�C��������y=ax2+bx+c����B��C���㣬��x�Ḻ���ύ�ڵ�A������AC��A(-1,0)
��1���������ߵĽ���ʽ��
��2����P��m��n�������������ڵ�һ�����ڵ�һ�㣬���ı���OCPB���S����m�ĺ�������ʽ��S�����ֵ��
��3����MΪ�����ߵĶ��㣬��Q��ֱ��BC�ϣ���N��ֱ��BM�ϣ�Q��M��N���㹹����MNΪ�ױߵĵ���ֱ�������Σ����N�����꣮

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��̽����
��1��һ�����������ͼ�ε�����ͼ������ͼ����ͼ1����ʾ��
���������������ǣ�ͼ2���ס����е��� ����
������������������� ����С�����幹�ɣ�����ͼ3�л���������������һ������ͼ��
��2����ͼ����֪һƽ���ڵ��ĸ���A��B��C��D������Ҫ����ֱ��ͼ��
�ٻ��߶�AB������AD��
����һ��M��ʹM�㼴������AD�ϣ�����ֱ��BC�ϣ�
����һ��N��ʹN��A��B��C��D�ĸ���ľ������̣�


�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ֱ��![]() �ֱ���x�ᡢy�ύ��
�ֱ���x�ᡢy�ύ��![]() ���㣬��ֱ��
���㣬��ֱ��![]() ���ڵ�C��4��2����
���ڵ�C��4��2����
��1����A������ �� ����B�� �� ����
��2�����߶�![]() ����һ��E������E��y���ƽ���߽�ֱ��
����һ��E������E��y���ƽ���߽�ֱ��![]() �ڵ�F�����E�ĺ�����Ϊm����mΪ��ֵʱ���ı���
�ڵ�F�����E�ĺ�����Ϊm����mΪ��ֵʱ���ı���![]() ��ƽ���ı��Σ�
��ƽ���ı��Σ�
��3������PΪx����һ�㣬����ƽ��ֱ������ϵ���Ƿ����һ��Q��ʹ��![]() �ĸ����ܹ���һ�����Σ������ڣ�������з���������Q�����ꣻ�������ڣ���˵�����ɣ�
�ĸ����ܹ���һ�����Σ������ڣ�������з���������Q�����ꣻ�������ڣ���˵�����ɣ�

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���±���ij����������������Ŀģ�⿼��ʱ10��ͬѧ�IJ��Գɼ�����λ����/���ӣ�
�ɼ�����/���ӣ� | 140 | 160 | 169 | 170 | 177 | 180 |
���� | 1 | 1 | 1 | 2 | 3 | 2 |
�������10��ͬѧÿ���������IJ��Գɼ�������˵��������ǣ� ��
A.������135B.ƽ������170C.��λ����173.5D.������177
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����P�ӣ�0��2������������ʾ�ķ����˶���ÿ���������εı�ʱ����������ʱ����ǵ�������ǣ�����P��2019���������εı�ʱ��P������Ϊ��������
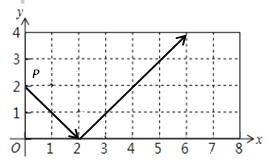
A.�� 2��4 ��B.�� 2��0 ��C.�� 8��2��D.�� 6��0 ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڡ�ABC�У���C= 90����D��BC����һ�㣬��DBΪֱ���ġ�O����AB���е�E����AD���ӳ����ڵ�F������EF��
��1����֤����1= ��F��
��2����CD= 3��EF=![]() �����O�İ뾶����
�����O�İ뾶����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���߹���ͼ����д��������Ҫ������ͼ�ۼ���

��1����֪���߶�a�͡�������ͼ����������ABC��ʹ��AB=a����ABC=��������BAC=2������
��2���ڣ�1���������£�����ABC=360�����ACB�Ķ���.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
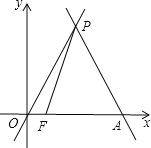
����Ŀ����֪����ͼ��ֱ��y����![]() x+4
x+4![]() ��x���ཻ�ڵ�A����ֱ��y��
��x���ཻ�ڵ�A����ֱ��y��![]() x���ڵ�P��
x���ڵ�P��
��1�����P�����꣮
��2������F��ԭ��O��������ÿ��1����λ���ٶ����߶�OA�����A�������˶�������PF�����˶�ʱ��Ϊt�룬��PFA�����ΪS�����S����t�ĺ�����ϵʽ��
��3������M��y��������һ�㣬��N������ƽ��������һ�㣬����O��M��N��PΪ������ı��������Σ���ֱ��д����N�����꣮
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com