
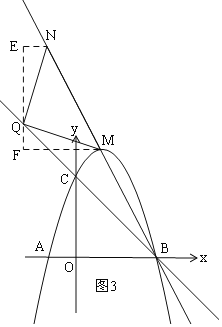
����Ŀ����ͼ����ƽ��ֱ������ϵ�У�ֱ��y=��x+3��x�ύ�ڵ�B����y�ύ�ڵ�C��������y=ax2+bx+c����B��C���㣬��x�Ḻ���ύ�ڵ�A������AC��A(-1,0)
��1���������ߵĽ���ʽ��
��2����P��m��n�������������ڵ�һ�����ڵ�һ�㣬���ı���OCPB���S����m�ĺ�������ʽ��S�����ֵ��
��3����MΪ�����ߵĶ��㣬��Q��ֱ��BC�ϣ���N��ֱ��BM�ϣ�Q��M��N���㹹����MNΪ�ױߵĵ���ֱ�������Σ����N�����꣮

���𰸡���1��y==��x2+2x+3����2��S=��![]() ��m��
��m��![]() ��2+
��2+![]() ����m=
����m=![]() ʱ��S�����ֵ��
ʱ��S�����ֵ��![]() ����3����N������Ϊ��2��2����1��8��
����3����N��������2��2����1��8��
�������������������1���ȸ���ֱ��BC�Ľ���ʽ�����B��C�����꣬�����ô���ϵ�����������ߵĽ���ʽ��
��2��������PE��������������ı���OCPB���S�����䷽�ɶ���ʽ��������ֵ��
��3���Ƚ��������䷽�ɶ���ʽ��M��1��4�������ô���ϵ������ֱ��MB�Ľ���ʽ�����ý���ʽ�ֱ��ʾN��Q��������ꣻ
������������ٵ�N������MB��ʱ����ͼ2��
��Q��EF��y�ᣬ�ֱ��M��N��x���ƽ���ߣ���EF��E��F��֤����EMQ�ա�FQN������ȫ�������ε�����EM=FQ��EQ=FN���з����������ɣ�
�ڵ�N������BM��ʱ����ͼ3��ͬ������õ�N�����꣮
�����������1����ֱ��y=��x+3��x�ύ�ڵ�B����y�ύ�ڵ�C��
�൱x=0ʱ��y=3��
��C��0��3����
��OC=3��
��y=0ʱ��-x+3=0��
x=3��
��B��3��0����
�������ߵĽ���ʽΪ��y=a��x+1����x-3����
��C��0��3������ã�3=a��0+1����0-3����
a=-1��
��y=-��x+1����x-3��=-x2+2x+3��
��2����ͼ1����P��PE��x����E��
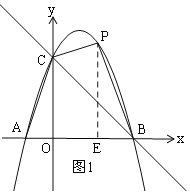
��P��m��n����
��OE=m��BE=3-m��PE=n��
S=S����COEP+S��PEB=![]() OE��PE+OC��+
OE��PE+OC��+![]() BEPE��
BEPE��
=![]() m��n+3��+
m��n+3��+![]() n��3-m����
n��3-m����
=![]() m+
m+![]() n��
n��
��n=-m2+2m+3��
��S=![]() m+
m+![]() ��-m2+2m+3��=-
��-m2+2m+3��=-![]() m2+
m2+![]() m+
m+![]() =-
=-![]() ��m-
��m-![]() ��2+
��2+![]() ��
��
��m=![]() ʱ��S�����ֵ��
ʱ��S�����ֵ��![]() ��
��
��3��y=-x2+2x+3=-��x-1��2+4��
��M��1��4����
��ֱ��BM�Ľ���ʽΪ��y=kx+b��
��B��3��0����M��1��4������ã� ![]() ����ã�
����ã� ![]() ��
��
��ֱ��BM�Ľ���ʽΪ��y=-2x+6��
��N��a��-2a+6����Q��n��-n+3����
�����������
�ٵ�N������MB��ʱ����ͼ2��
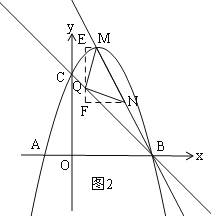
��Q��EF��y�ᣬ�ֱ��M��N��x���ƽ���ߣ���EF��E��F��
�ߡ�EQN�ǵ���ֱ�������Σ�
��MQ=QN����MQN=90����
���EQM+��FQN=90����
�ߡ�EQM+��EMQ=90����
���FQN=��EMQ��
�ߡ�QEM=��QFN=90����
���EMQ�ա�FQN��
��EM=FQ��EQ=FN��
��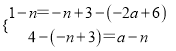 ����ã�
����ã� 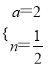 ��
��
��a=2ʱ��y=-2a+6=-2��2+6=2��
��N��2��2����
�ڵ�N������BM��ʱ����ͼ3��
ͬ���������ߣ�����ENQ�ա�FQM��
��EN=FQ��EQ=FM��
��![]() ����ã�
����ã� ![]() ��
��
��N��-1��8����
������������N��������2��2����-1��8����


 Ӧ�����������Ĵ���ѧ������ϵ�д�
Ӧ�����������Ĵ���ѧ������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������������![]() �ĵױ�
�ĵױ�![]() ��Ϊ6�������36����
��Ϊ6�������36����![]() �Ĵ�ֱƽ����
�Ĵ�ֱƽ����![]() �ֱ�
�ֱ�![]() ��
��![]() ����
����![]() ��
��![]() �㣬����
�㣬����![]() Ϊ
Ϊ![]() �ߵ��е㣬��
�ߵ��е㣬��![]() Ϊ�߶�
Ϊ�߶�![]() ��һ���㣬��
��һ���㣬��![]() �ܳ�����Сֵ____��
�ܳ�����Сֵ____��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪һ��ֱ�������ε�����ֱ�DZ߷ֱ�Ϊ6��8����ô���ֱ��������б���ϵĸ�Ϊ__�������ε����߷ֱ�Ϊ3��5Ҫʹ������������ֱ�������Σ�������߳���__��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
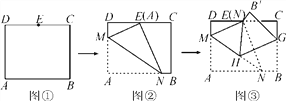
����Ŀ����ͼ1���ı���ABCD�������Σ���G��BC��������һ�㣮DE��AG�ڵ�E��BF��DE�ҽ�AG�ڵ�F��

��1����֤��AE��BF��
��2����ͼ2�������G��BC�ӳ�����һ�㣬�����������䣬���߶�AF��BF��EF��ʲô������ϵ����֤������Ľ��ۣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij���о���һ�����۳ɱ�Ϊÿ��60Ԫ����Ʒ�����г����鷢�֣������ÿ��70Ԫ���ۣ�һ�����۳�500���������۵���ÿ��1Ԫ��ÿ�����۾ͼ���10���������ۼ�Ϊÿ��xԪ��x��70����һ�ܵ�������Ϊy��.
��1�������ۼ�Ϊÿ��80Ԫʱ��һ�������۶��ټ�����_____________����
��2��д��y��x�ĺ�����ϵʽ����д��x��ȡֵ��Χ.
��3����һ�ܵ���������Ϊw��д��w��x�ĺ�����ϵʽ.
��4���ڳ��жԸ�����ƷͶ�벻����18000Ԫ������£�ʹ��һ����������ﵽ8000Ԫ�����۵���Ӧ��Ϊ���٣�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ھ���ABCD����AB��8![]() ��AD��10����E��CD���е���������ֽƬ�����۵����Σ���һ���۵�ֽƬʹ��A���E�غ�����ͼ�����ۺ�ΪMN������ME��NE���ڶ����۵�ֽƬʹ��N���E�غ�����ͼ������B�䵽B�������ۺ�ΪHG������HE�������н��ۣ���ME��HG���ڡ�MEH�ǵȱ����������ۡ�EHG����AMN����tan��EHG��
��AD��10����E��CD���е���������ֽƬ�����۵����Σ���һ���۵�ֽƬʹ��A���E�غ�����ͼ�����ۺ�ΪMN������ME��NE���ڶ����۵�ֽƬʹ��N���E�غ�����ͼ������B�䵽B�������ۺ�ΪHG������HE�������н��ۣ���ME��HG���ڡ�MEH�ǵȱ����������ۡ�EHG����AMN����tan��EHG��![]() .������ȷ�ĸ�����(�� ��)
.������ȷ�ĸ�����(�� ��)
A. 1�� B. 2�� C. 3�� D. 4��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��ijУ��ѧ¥AB����һб�£���֪б��CD�ij�Ϊ12�ף��½Ǧ�Ϊ60�㣬�����йز��ŵĹ涨���Ϧ���39��ʱ�����ܱ��⻬��Σ�գ�ѧУΪ��������ȫ������������б��CD���и��죬�ڱ����½�C����������£�ѧУ����Ҫ���¶�D���ˮƽ�ƶ������ײ��ܱ�֤��ѧ¥�İ�ȫ�������ȡ������
���ο����ݣ�sin39���0.63��cos39���0.78��tan39���0.81��![]() ��1.41��
��1.41��![]() ��1.73��
��1.73��![]() ��2.24��
��2.24��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����������ABCD�У�AB=8����P�ڱ�CD�ϣ�tan��PBC=![]() ����Q��������BP�ϵ�һ�����㣬����Q��AB��ƽ���߽�����AD�ڵ�M����R������AD�ϣ�ʹRQʼ����ֱ��BP��ֱ��
����Q��������BP�ϵ�һ�����㣬����Q��AB��ƽ���߽�����AD�ڵ�M����R������AD�ϣ�ʹRQʼ����ֱ��BP��ֱ��
��1����ͼ1������R���D�غ�ʱ����PQ�ij���
��2����ͼ2����̽���� ![]() �ı�ֵ�Ƿ����Q���˶��������仯�����б仯����˵��������ɣ���û�б仯����������ı�ֵ��
�ı�ֵ�Ƿ����Q���˶��������仯�����б仯����˵��������ɣ���û�б仯����������ı�ֵ��
��3����ͼ3������Q���߶�BP�ϣ���PQ=x��RM=y����y����x�ĺ�����ϵʽ����д�����Ķ�����

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���������������a��b��cΪһ�鹴��������ô4a��4b��4c���ǹ�����������������ε������ڽǵĶ�������3��4��5����ô�����������ֱ�������Σ������һ�������ε�������12��25��21����ô�������α���ֱ�������Σ���һ������ֱ�������ε�������a��b��c����a��b��c������ôa2��b2��c2��2��1��1��������ȷ���ǣ�������
A.�٢�B.�٢�C.�٢�D.�ڢ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com