
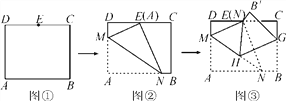
【题目】如图,在矩形ABCD中,AB=8![]() ,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图②,折痕为MN,连接ME,NE;第二次折叠纸片使点N与点E重合,如图③,点B落到B′处,折痕为HG,连接HE,则下列结论:①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=
,AD=10,点E是CD的中点,将这张纸片依次折叠两次:第一次折叠纸片使点A与点E重合,如图②,折痕为MN,连接ME,NE;第二次折叠纸片使点N与点E重合,如图③,点B落到B′处,折痕为HG,连接HE,则下列结论:①ME∥HG;②△MEH是等边三角形;③∠EHG=∠AMN;④tan∠EHG=![]() .其中正确的个数是( )
.其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
【答案】C
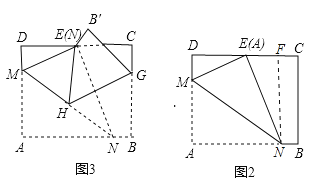
【解析】解:如图③,由折叠可得,∠MEN=∠A=90°,HG⊥NE,即ME⊥EN,HG⊥EN,∴EM∥GH,故①正确;
∵EM∥GH,∴∠NME=∠NHG,由折叠可得,∠NME=∠AMN,∠EHG=∠NHG,∴∠AMN=∠EHG,故③正确;
如图2,作NF⊥CD于F.设DM=x,则AM=EM=10﹣x.∵点E是CD的中点,AB=CD=![]() ,∴DE=
,∴DE=![]() CD=
CD=![]() .在Rt△DEM中,∵DM2+DE2=EM2,∴(
.在Rt△DEM中,∵DM2+DE2=EM2,∴(![]() )2+x2=(10﹣x)2,解得x=2.6,∴DM=2.6,AM=EM=7.4.∵∠DEM+∠NEF=90°,∠NEF+∠ENF=90°,∴∠DEM=∠ENF.∵∠D=∠EFN=90°,∴△DME∽△FEN,∴
)2+x2=(10﹣x)2,解得x=2.6,∴DM=2.6,AM=EM=7.4.∵∠DEM+∠NEF=90°,∠NEF+∠ENF=90°,∴∠DEM=∠ENF.∵∠D=∠EFN=90°,∴△DME∽△FEN,∴![]() ,即
,即![]() ,∴EN=
,∴EN=![]() ,∴AN=
,∴AN=![]() ,∴tan∠AMN=
,∴tan∠AMN=![]() =
=![]() ,∴tan∠EHG=
,∴tan∠EHG=![]() ,故④正确;
,故④正确;
又∵tan60°=![]() >
>![]() ,∴∠AMN≠60°,即∠EMH≠60°,∴△MEH不是等边三角形,故②错误,∴正确的结论有3个.故选C.
,∴∠AMN≠60°,即∠EMH≠60°,∴△MEH不是等边三角形,故②错误,∴正确的结论有3个.故选C.


 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F,∠1=∠2.
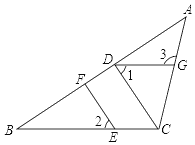
(1)试说明DG∥BC的理由;
(2)如果∠B=34°,且∠ACD=47°,求∠3的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在△ABC 中,AD平分∠BAC,AE⊥BC,∠B=40°,∠C=70°.
(1)求∠DAE的度数;
(2)如图②,若把“AE⊥BC”变成“点F在DA的延长线上,FE⊥BC”,其它条件不变,求∠DFE的度数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中.直线y=﹣x+3与x轴交于点B,与y轴交于点C,抛物线y=ax2+bx+c经过B,C两点,与x轴负半轴交于点A,连结AC,A(-1,0)
(1)求抛物线的解析式;
(2)点P(m,n)是抛物线上在第一象限内的一点,求四边形OCPB面积S关于m的函数表达式及S的最大值;
(3)若M为抛物线的顶点,点Q在直线BC上,点N在直线BM上,Q,M,N三点构成以MN为底边的等腰直角三角形,求点N的坐标.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,如图点P是△ABC的边BC上的一动点,点E与点P关于直线AB成轴对称,连接EP交AB于点F,连接AP、EC相交于点O,连接AE.

(1)判断AE与AP的数量关系,并说明理由.
(2)在点P的运动过程中,当AE∥BC时,判断AP与BP的数量关系,并说明理由.
(3)若∠BAC=900,点P在运动过程中是否存在线段AP与线段EC互相平分的情况,若存在,请求出点P的位置;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】两个少年在绿茵场上游戏.小红从点A出发沿线段AB运动到点B,小兰从点C出发,以相同的速度沿⊙O逆时针运动一周回到点C,两人的运动路线如图1所示,其中AC![]() DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )
DB.两人同时开始运动,直到都停止运动时游戏结束,其间他们与点C的距离y与时间x(单位:秒)的对应关系如图2所示.则下列说法正确的是( )


A. 小红的运动路程比小兰的长
B. 两人分别在1.09秒和7.49秒的时刻相遇
C. 当小红运动到点D的时候,小兰已经经过了点D
D. 在4.84秒时,两人的距离正好等于⊙O的半径
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点P从(0,2)出发,沿所示的方向运动,每当碰到矩形的边时反弹,反弹时反射角等于入射角,当点P第2019次碰到矩形的边时点P的坐标为( )
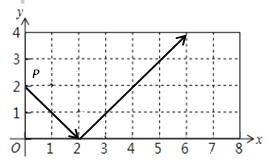
A.( 2,4 )B.( 2,0 )C.( 8,2)D.( 6,0 )
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com