
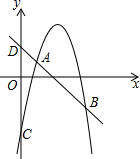
 ŅŃÖŖ£ŗÅ×ĪļĻßy=-x2+bx+cµÄĶ¼Ļó½»yÖįÓŚµćC£¬Ņ»“ĪŗÆŹży=-x+m½»yÖįÓŚµćD£¬½»Å×ĪļĻßÓŚA”¢BĮ½µć£¬B£Ø6£¬-3£©£¬ĒŅAB=2AD£®
ŅŃÖŖ£ŗÅ×ĪļĻßy=-x2+bx+cµÄĶ¼Ļó½»yÖįÓŚµćC£¬Ņ»“ĪŗÆŹży=-x+m½»yÖįÓŚµćD£¬½»Å×ĪļĻßÓŚA”¢BĮ½µć£¬B£Ø6£¬-3£©£¬ĒŅAB=2AD£®·ÖĪö £Ø1£©½«µćBµÄ×ų±ź“śČėÖ±ĻߵĽāĪöŹ½æÉĒóµĆm=3£¬æɵƵ½Ņ»“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy=-x+3£¬“Ó¶ųæÉĒóµĆµćDµÄ×ų±źĪŖ£Ø0£¬3£©ÓÉAB=2ADæÉĒóµĆµćAµÄ×ų±źĪŖ£Ø2£¬1£©£¬Č»ŗ󽫵ćA”¢BµÄ×ų±ź“śČėÖ±ĻߵĽāĪöŹ½£¬æÉĒóµĆb”¢cµÄÖµ£»
£Ø2£©½«µćx=n“śČėŅ»“ĪŗÆŹżµÄ½āĪöŹ½æÉĒóµĆµćPµÄׯ×ų±ź£¬½«x=n“śČėÅ×ĪļĻߵĽāĪöŹ½æÉĒóµĆµćQµÄׯ×ų±ź£¬“Ó¶ųæɵƵ½QPµÄ³¤¶Č£¬Č»ŗóŅĄ¾ŻČż½ĒŠĪµÄĆ껿¹«Ź½æÉĮŠ³öSÓėnµÄŗÆŹż¹ŲĻµŹ½£»
£Ø3£©×÷Ō²E¹żµćA”¢Q”¢B£¬Ō²E½»QPÓŚµćF£¬×÷µćF¹ŲÓŚABµÄ¶Ō³ĘµćF”䣬Óɶž“ĪŗÆŹżµÄŠŌÖŹæÉÖŖµ±µćPµÄ×ų±źĪŖ£Ø4£¬-1£©Ź±£¬SÓŠ×ī“óÖµ£¬Č»ŗóĒóµĆAQ”¢AB”¢BQµÄ³¤¶Č£¬ŅĄ¾Ż¹“¹É¶ØĄķµÄÄę¶ØĄķæÉÖŖ”÷ABQĪŖÖ±½ĒČż½ĒŠĪ£¬“Ó¶ųæÉÖŖµćEŌŚxÖįÉĻ£¬ÓÉ“¹¾¶¶ØĄķæÉĒóµĆµćFµÄ×ų±ź£¬ĄūÓĆ“ż¶ØĻµŹż·ØæÉĒóµĆAFµÄ½āĪöŹ½£¬Č»ŗóÖ±ĻßAFÓėÅ×ĪļĻߵĽ»µć×ų±ź¼“æÉĒóµĆRµÄ×ų±ź£¬ÓÉÖį¶Ō³ĘµÄŠŌÖŹæÉĒóµĆµćF”äµÄ×ų±ź£¬Ķ¬ĄķæÉĒóµĆÖ±ĻßAF”äÓėÅ×ĪļĻߵĽ»µć×ų±ź£¬“Ó¶ųæÉĒóµĆµćRµÄ×ų±ź£®
½ā“š ½ā£ŗ£Ø1£©”ßµćB£Ø6£¬-3£©ŌŚÖ±Ļßy=-x+mÉĻ£¬
”ą-6+m=-3£®
½āµĆ£ŗm=3£®
”ąŅ»“ĪŗÆŹżµÄ½āĪöŹ½ĪŖy=-x+3£®
”ąµćDµÄ×ų±źĪŖ£Ø0£¬3£©£®
Ó֔ߵćB£Ø6£¬-3£©£¬ĒŅAB=2AD£¬
”ąµćAµÄ×ų±źĪŖ£Ø2£¬1£©£®
½«µćA”¢BµÄ×ų±ź“śČėÅ×ĪļĻߵĽāĪöŹ½µĆ£ŗ$\left\{\begin{array}{l}{-4+2b+c=1}\\{-36+6b+c=-3}\end{array}\right.$£¬
½āµĆ£ŗ$\left\{\begin{array}{l}{b=7}\\{c=-9}\end{array}\right.$£®
”ąÅ×ĪļĻߵĽāĪöŹ½ĪŖy=-x2+7x-9£®
£Ø2£©ČēĶ¼1ĖłŹ¾£ŗ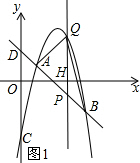
”ßµćPµÄŗį×ų±źĪŖn£¬
”ąµćPµÄׯ×ų±źĪŖ-n+3£¬µćQµÄׯ×ų±źĪŖ-n2+7n-9£®
”ąQP=-n2+7n-9-£Ø-n+3£©=-n2+8n-12£®
”ß”÷AQBµÄĆ껿ĪŖS=$\frac{1}{2}QP”Į£Ø{B}_{x}-{A}_{x}£©$£¬
”ąS=$\frac{1}{2}”Į4”Į$£Ø-n2+8n-12£©=-2n2+16n-24£®
”ąSÓėnµÄŗÆŹż¹ŲĻµŹ½ĪŖS=-2n2+16n-24£Ø2£¼n£¼6£©£®
£Ø3£©µ±n=-$\frac{b}{2a}$=-$\frac{16}{-2”Į2}$=4Ź±£¬SÓŠ×ī“óÖµ£®
”ąµćPµÄ×ų±źĪŖ£Ø4£¬-1£©£¬µćQµÄ×ų±źĪŖ£Ø4£¬3£©£®
ČēĶ¼2ĖłŹ¾£¬×÷Ō²E¹żµćA”¢Q”¢B£¬Ō²E½»QPÓŚµćF£¬×÷µćF¹ŲÓŚABµÄ¶Ō³ĘµćF”䣮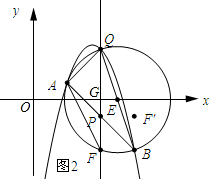
”ßÓÉĮ½µćÖ®¼äµÄ¾ąĄė¹«Ź½æÉÖŖ£»AQ2=£Ø4-2£©2+£Ø3-1£©2=8£»QB2=£Ø6-4£©2+£Ø-3-3£©2=40£»AB2=£Ø6-2£©2+£Ø-3-1£©2=32£®
”ąAQ2+AB2=QB2£®
”ą”÷AQBĪŖÖ±½ĒČż½ĒŠĪ£®
”ąQBĪŖŌ²EµÄÖ±¾¶£®
”ąEĪŖQ”¢BµÄÖŠµć£®
”ąµćEµÄ×ų±źĪŖ£Ø5£¬0£©£®
”ßµćEŌŚxÖįÉĻ£¬QP”ĶxÖį£¬
”ąQG=FG£®
”ąµćFµÄ×ų±źĪŖ£Ø4£¬-3£©£®
ÉčÖ±ĻßAFµÄ½āĪöŹ½ĪŖy=kx+b£¬øł¾ŻĢāŅāµĆ£ŗ$\left\{\begin{array}{l}{4k+b=-3}\\{2k+b=1}\end{array}\right.$£®
½āµĆ£ŗ$\left\{\begin{array}{l}{k=-2}\\{b=5}\end{array}\right.$£®
”ąÖ±ĻßAFµÄ½āĪöŹ½ĪŖy=-2x+5£®
½«y=-2x+5Óėy=-x2+7x-9ĮŖĮ¢½āµĆ£ŗ$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=1}\end{array}\right.$£¬$\left\{\begin{array}{l}{{x}_{2}=7}\\{{y}_{2}=-9}\end{array}\right.$£®
”ąRµÄ×ų±źĪŖ£Ø7£¬-9£©£®
”ßµćF”äÓėµćF¹ŲÓŚAB¶Ō³Ę£¬
”ąµćF”äµÄ×ų±źĪŖ£Ø6£¬-1£©£®
ÉčÖ±ĻßAF”äµÄ½āĪöŹ½ĪŖy=k1x+b1£¬øł¾ŻĢāŅāµĆ£ŗ$\left\{\begin{array}{l}{6{k}_{1}+{b}_{1}=-1}\\{2{k}_{1}+{b}_{1}=1}\end{array}\right.$£®
½āµĆ£ŗ${k}_{1}=-\frac{1}{2}$£¬b1=2£®
”ąÖ±ĻßAF”äµÄ½āĪöŹ½ĪŖy=$-\frac{1}{2}x$+2£®
½«y=$-\frac{1}{2}x$+2Óėy=-x2+7x-9ĮŖĮ¢½āµĆ$\left\{\begin{array}{l}{{x}_{1}=2}\\{{y}_{1}=1}\end{array}\right.$£¬$\left\{\begin{array}{l}{{x}_{2}=5.5}\\{{y}_{2}=-\frac{3}{4}}\end{array}\right.$£®
”ąRµÄ×ų±źĪŖ£Ø5.5£¬-$\frac{3}{4}$£©£®
×ŪÉĻĖłŹö£¬µćRµÄ×ų±źĪŖ£Ø5.5£¬-$\frac{3}{4}$£©»ņ£Ø7£¬-9£©£®
µćĘĄ ±¾ĢāÖ÷ŅŖæ¼²éµÄŹĒ¶ž“ĪŗÆŹżµÄ×ŪŗĻÓ¦ÓĆ£¬½ā“š±¾ĢāÖ÷ŅŖÓ¦ÓĆĮĖ¶ž“ĪŗÆŹżµÄĶ¼ĻóŗĶŠŌÖŹ”¢¹“¹É¶ØĄķµÄÄę¶ØĄķ”¢Į½µć¼äµÄ¾ąĄė¹«Ź½”¢Ō²µÄŠŌÖŹ”¢“ż¶ØĻµŹż·ØĒóŗÆŹżµÄ½āĪöŹ½”¢“¹¾¶¶ØĄķ£¬¹¹Ōģ³ö¹żµćA”¢B”¢QČżµćµÄŌ²ŹĒ½āĢāµÄ¹Ų¼ü£®



| Äź¼¶ | øßÖŠæĪ³Ģ | Äź¼¶ | ³õÖŠæĪ³Ģ |
| øßŅ» | øßŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” | ³õŅ» | ³õŅ»Ćā·ŃæĪ³ĢĶĘ¼ö£” |
| ø߶ž | ø߶žĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õ¶ž | ³õ¶žĆā·ŃæĪ³ĢĶĘ¼ö£” |
| øßČż | øßČżĆā·ŃæĪ³ĢĶĘ¼ö£” | ³õČż | ³õČżĆā·ŃæĪ³ĢĶĘ¼ö£” |
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗŃ”ŌńĢā
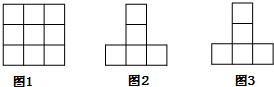 ½«Ņ»Š©Ąā³¤ĪŖ1µÄÕż·½Ģå°Ś·ÅŌŚ3”Į3µÄĘ½ĆęÉĻ£ØČēĶ¼1ĖłŹ¾£©£¬ĘäÕżŹÓĶ¼ŗĶ²ąŹÓĶ¼·Ö±šČēĶ¼2”¢Ķ¼3£¬¼Ē°Ś·ÅµÄÕż·½ĢåøöŹżµÄ×ī“óÖµĪŖm£¬×īŠ”ÖµĪŖn£¬Ōņm-n=£Ø””””£©
½«Ņ»Š©Ąā³¤ĪŖ1µÄÕż·½Ģå°Ś·ÅŌŚ3”Į3µÄĘ½ĆęÉĻ£ØČēĶ¼1ĖłŹ¾£©£¬ĘäÕżŹÓĶ¼ŗĶ²ąŹÓĶ¼·Ö±šČēĶ¼2”¢Ķ¼3£¬¼Ē°Ś·ÅµÄÕż·½ĢåøöŹżµÄ×ī“óÖµĪŖm£¬×īŠ”ÖµĪŖn£¬Ōņm-n=£Ø””””£©| A£® | 4 | B£® | 5 | C£® | 6 | D£® | 7 |
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
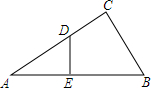 ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻACB=90”ć£¬DĪŖACÉĻŅ»µć£¬DE”ĶABÓŚµćE£¬AC=12£¬BC=5£®
ČēĶ¼£¬ŌŚ”÷ABCÖŠ£¬”ĻACB=90”ć£¬DĪŖACÉĻŅ»µć£¬DE”ĶABÓŚµćE£¬AC=12£¬BC=5£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
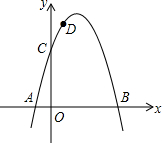 ČēĶ¼£¬¶ž“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄĶ¼ĻóÓėxÖį½»ÓŚA£Ø-1£¬0£©£¬BĮ½µć£¬ÓėyÖį½»ÓŚµćC£Ø0£¬5£©£¬µćD£Ø1£¬8£©ŌŚÅ×ĪļĻßÉĻ£¬ĒóÅ×ĪļĻ߶ŌÓ¦µÄŗÆŹż±ķ“ļŹ½£®
ČēĶ¼£¬¶ž“ĪŗÆŹży=ax2+bx+c£Øa”Ł0£©µÄĶ¼ĻóÓėxÖį½»ÓŚA£Ø-1£¬0£©£¬BĮ½µć£¬ÓėyÖį½»ÓŚµćC£Ø0£¬5£©£¬µćD£Ø1£¬8£©ŌŚÅ×ĪļĻßÉĻ£¬ĒóÅ×ĪļĻ߶ŌÓ¦µÄŗÆŹż±ķ“ļŹ½£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗĢīæÕĢā
²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
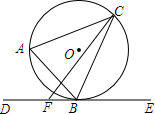 ČēĶ¼£¬”÷ABCÄŚ½ÓÓŚ”ŃO£¬¹żµćB×÷”ŃOµÄĒŠĻßDE£¬FĪŖÉäĻßBDÉĻŅ»µć£¬Į¬½ÓCF£®
ČēĶ¼£¬”÷ABCÄŚ½ÓÓŚ”ŃO£¬¹żµćB×÷”ŃOµÄĒŠĻßDE£¬FĪŖÉäĻßBDÉĻŅ»µć£¬Į¬½ÓCF£®²éæ““š°øŗĶ½āĪö>>
æĘÄæ£ŗ³õÖŠŹżŃ§ Ą“Ō“£ŗ ĢāŠĶ£ŗ½ā“šĢā
²éæ““š°øŗĶ½āĪö>>
¹ś¼ŹŃ§Š£ÓÅŃ” - Į·Ļ°²įĮŠ±ķ - ŹŌĢāĮŠ±ķ
ŗž±±Ź”»„ĮŖĶųĪ„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±ØĘ½ĢØ | ĶųÉĻÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | µēŠÅÕ©Ę¾Ł±Ø×ØĒų | É꥜Ź·ŠéĪŽÖ÷ŅåÓŠŗ¦ŠÅĻ¢¾Ł±Ø×ØĒų | ÉęĘóĒÖČؾŁ±Ø×ØĒų
Ī„·ØŗĶ²»Į¼ŠÅĻ¢¾Ł±Øµē»°£ŗ027-86699610 ¾Ł±ØÓŹĻä£ŗ58377363@163.com