
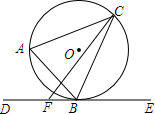
 如图,△ABC内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF.
如图,△ABC内接于⊙O,过点B作⊙O的切线DE,F为射线BD上一点,连接CF.分析 (1)连接BO并延长交⊙O于点M,连接MC,根据圆周角定理求出∠A=∠M,∠MCB=90°,求出∠M+∠MBC=90°,根据切线性质求出∠CBE+∠MBC=90°,推出∠CBE=∠M即可;
(2)过点C作CN⊥DE于点N,求出∠CNF=90°,求出tanM=tan∠CBE=tanA=2,解直角三角形求出BC、CN、BN,求出FN,根据勾股定理求出即可.
解答 (1)证明:如图,连接BO并延长交⊙O于点M,连接MC,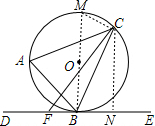
∴∠A=∠M,∠MCB=90°,
∴∠M+∠MBC=90°,
∵DE是⊙O的切线,
∴∠CBE+∠MBC=90°,
∴∠CBE=∠M,
∴∠CBE=∠A;
(2)解:过点C作CN⊥DE于点N,
∴∠CNF=90°,
由(1)得,∠M=∠CBE=∠A,
∴tanM=tan∠CBE=tanA=2,
在Rt△BCM中,
∵BM=5,tanM=2,
∴$BC=2\sqrt{5}$,
在Rt△CNB中,
∵$BC=2\sqrt{5},tan∠CBE=2$,
∴CN=4,BN=2,
∵BF=2,
∴FN=BF+BN=4,
在Rt△FNC中,
∵FN=4,CN=4,
∴$CF=4\sqrt{2}$.
点评 本题考查了解直角三角形,勾股定理,切线的性质,圆周角定理的应用,能求出∠M=∠CBE=∠A是解此题的关键,题目比较好,难度偏大.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
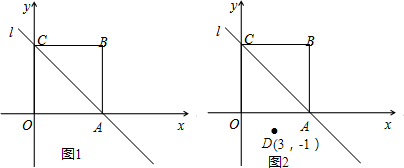
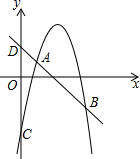 已知:抛物线y=-x2+bx+c的图象交y轴于点C,一次函数y=-x+m交y轴于点D,交抛物线于A、B两点,B(6,-3),且AB=2AD.
已知:抛物线y=-x2+bx+c的图象交y轴于点C,一次函数y=-x+m交y轴于点D,交抛物线于A、B两点,B(6,-3),且AB=2AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
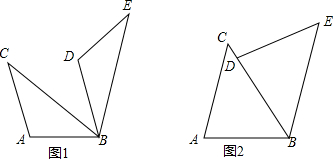
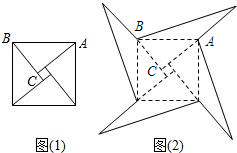 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )| A. | 76 | B. | 72 | C. | 68 | D. | 52 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com