

���� ��1����������ֱ�߽���ʽ���������C���꼴�ɣ�����ֱ��y=-2x+12�����A�����꣬ȷ����OA�ij�����ΪC�������꣬���������OAC������ɣ�
��2����OA�ij����Լ�������OAC����������C�������꣬����y=xȷ����C�����꣬��ֱ��AB����ʽΪy=kx+b����A��C����������k��b��ֵ������ȷ����ֱ��AB����ʽ��
��3����ONΪ��ƽ���ߣ��õ�һ�Խ���ȣ�����AB��ON��ֱ���õ�һ��ֱ����ȣ�����OEΪ�����ߣ�����ASA�õ�������AOE��������COEȫ�ȣ�����ȫ�������εĶ�Ӧ����ȵõ�CE=AE��OA=OC����C��CP��ֱ��OA����OE�ڵ�Q����ʱAQ+PQ��С����������Сֵ���ɣ�
��� �⣺��1���������ã�$\left\{\begin{array}{l}{y=-2x+12}\\{y=x}\end{array}\right.$��
��ȥy�ã�x=-2x+12��
��ã�x=4��
��x=4����ã�y=4��
��C��4��4����
�ڶ���ֱ��AB����ʽy=-2x+12��
��x=0���õ�y=12����y=0���õ�x=6��
��A��6��0����B��0��12������OA=6��
��S��AOC=$\frac{1}{2}$OA•y��C������=12��
��2����OA=4����AOC���Ϊ6��
���C������Ϊ3��
��y=3����y=x�ã�x=3����C��3��3����
��ֱ��AB����ʽΪy=kx+b��
��A��4��0����C��3��3������ã�$\left\{\begin{array}{l}{4k+b=0}\\{3k+b=3}\end{array}\right.$��
��ã�k=-3��b=12��
��ֱ��AB����ʽΪy=-3x+12��
��3����OEƽ�֡�AOC��OE��AC��
���AOE=��COE����AEO=��CEO=90�㣬
�ڡ�AOE�͡�COE�У�
$\left\{\begin{array}{l}{��AOE=��COE}\\{OE=OE}\\{��AEO=��CEO}\end{array}\right.$��
���AOE�ա�COE��ASA����
��AE=CE������A���C����OE�Գƣ�OC=OA=4��
��C��CP��OA����OE�ڵ�Q����ʱAQ+PQ��С����ͼ��ʾ��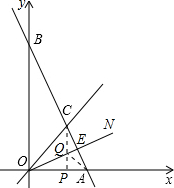
��C��3��3������OP=CP=3��
�ࣨAQ+PQ��min=CQ+PQ=CP=3��
���� ��������һ�κ����ۺ��⣬�漰��֪ʶ�У���ֱ�ߵĽ������꣬������ͼ�����ʣ�ȫ�������ε��ж������ʣ�һ�κ�����������Ľ��㣬�ԳƵ����ʣ��Լ�һ�κ��������ʣ������������㷨���������ǽⱾ��Ĺؼ���


 ������������ϵ�д�
������������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
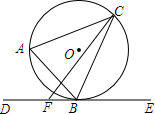 ��ͼ����ABC�ڽ��ڡ�O������B����O������DE��FΪ����BD��һ�㣬����CF��
��ͼ����ABC�ڽ��ڡ�O������B����O������DE��FΪ����BD��һ�㣬����CF���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
 �����뻯��
�����뻯���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | 2.1��105 | B�� | 2.1��106 | C�� | 21��105 | D�� | 0.21��107 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com