

分析 (1)连接OC,根据切线与圆的关系和直角三角形内角之间的关系,可以推出AC平分∠DAB;
(2)根据圆周角定理以及三角形的外角的性质定理证明∠ECG=∠EGC,根据等角对等边即可证得;
(3)证明△ECB∽△EAC,根据相似三角形的性质求得$\frac{EB}{EC}$=$\frac{BC}{AC}$=$\frac{3}{6}$=$\frac{1}{2}$,在直角△EOC中利用勾股定理列方程求得BE和CE,进而求得BG,然后根据△AGF∽△CGB,根据相似三角形的性质求得FG的长.
解答 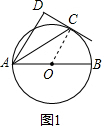 (1)证明:连接OC,如图1,
(1)证明:连接OC,如图1,
∴OC⊥DC,
∵AD⊥DC,
∴OC∥AD,
∴∠DAC=∠ACO,
∵∠OAC=∠OCA,
∴∠DAC=∠OAC,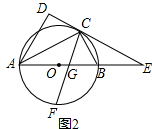 即AC平分∠DAB;
即AC平分∠DAB;
(2)证明:如图2,∵DE是⊙O的切线,
∴∠BCE=∠BAC,
∵∠EGC=∠BAC+∠ACG,∠ECG=∠BCE+∠BCG,∠ACG=∠BCG,
∴∠EGC=∠ECG,
∴EC=EG;
(3)解:如图3,连接AF、BF、OC.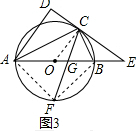
∵AB是直径,
∴∠ACB=90°,
∴AB=$\sqrt{A{C}^{2}+B{C}^{2}}$=$\sqrt{{6}^{2}+{3}^{2}}$=3$\sqrt{5}$,
∴OA=OB=OC=$\frac{3}{2}$$\sqrt{5}$,
∵∠ACF=∠BCF,
∴$\widehat{AF}$=$\widehat{BF}$,
∴AF=BF.
∵AB是直径,
∴∠AFB=90°.
∴AF=$\frac{\sqrt{2}}{2}$AB=$\frac{\sqrt{2}}{2}$×3$\sqrt{5}$=$\frac{3}{2}$$\sqrt{10}$,
∵∠ECB=∠EAC,∠E=∠E,
∴△ECB∽△EAC.
∴$\frac{EB}{EC}$=$\frac{BC}{AC}$=$\frac{3}{6}$=$\frac{1}{2}$.
设EB=x,则EC=2x,在Rt△EOC中,(x+$\frac{3}{2}$$\sqrt{5}$)2=(2x)2+($\frac{3}{2}$$\sqrt{5}$)2,
解得x1=0,x2=$\sqrt{5}$.
∵x>0,∴x=$\sqrt{5}$,
∴EB=$\sqrt{5}$,EG=CE=2$\sqrt{5}$,
∴BG=$\sqrt{5}$,
∵∠FAG=∠BCG,∠AGF=∠CGB,
∴△AGF∽△CGB,
∴$\frac{FG}{BG}$=$\frac{AF}{BC}$,即$\frac{FG}{\sqrt{5}}$=$\frac{\frac{3\sqrt{10}}{2}}{3}$,
∴FG=$\frac{5}{2}$$\sqrt{2}$.
点评 本题考查了圆的切线性质、三角形相似的判定和性质、及勾股定理的应用等知识.运用切线的性质来进行计算或论证,常通过作辅助线连接圆心和切点,利用垂直构造直角三角形解决有关问题.


 期末好成绩系列答案
期末好成绩系列答案 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:解答题
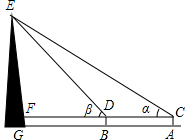 如图,小嘉利用测角仪测量塔高,他分别站在A、B两点测得塔顶的仰角α=45°,β=50°.AB为10米.已知小嘉的眼睛距地面的高度AC为1.5米,计算塔的高度.(参考数据:sin50°取0.8,cos50°取0.6,tan50°取1.2)
如图,小嘉利用测角仪测量塔高,他分别站在A、B两点测得塔顶的仰角α=45°,β=50°.AB为10米.已知小嘉的眼睛距地面的高度AC为1.5米,计算塔的高度.(参考数据:sin50°取0.8,cos50°取0.6,tan50°取1.2)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com