
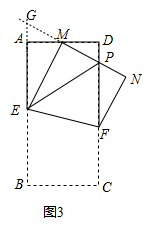
 ,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设
,其中m≥1,将该矩形沿EF折叠(点E、F分别在边AB、CD上),使点B落在AD边上的点M处,点C落在点N处,MN与CD相交于点P,连接EP.设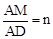 ,其中0<n≤1.
,其中0<n≤1.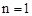 (即M点与D点重合),
(即M点与D点重合), 时,则
时,则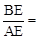 ;
;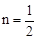 (M为AD的中点),m的值发生变化时,求证:
(M为AD的中点),m的值发生变化时,求证: ;
;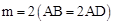 ,n的值发生变化时,
,n的值发生变化时,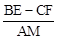 的值是否发生变化?说明理由.
的值是否发生变化?说明理由.
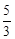 ;(2)证明见解析;(3)
;(2)证明见解析;(3)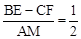 ,不发生变化,理由见解析.
,不发生变化,理由见解析.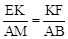 ,即
,即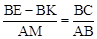 ,由AB=2AD=2BC,BK=CF就可以得出
,由AB=2AD=2BC,BK=CF就可以得出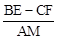 的值是
的值是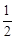 为定值.
为定值.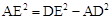 ,即
,即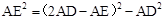 ,∴AE=
,∴AE=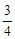 AD.
AD.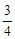 AD=
AD=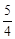 .
.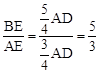 .
.
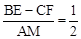 ,值不变,理由如下:
,值不变,理由如下: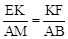 即
即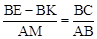 .
.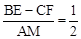 .
.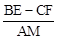 的值不变.
的值不变.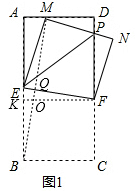


科目:初中数学 来源:不详 题型:解答题
 ,如图1所示,将△
,如图1所示,将△ 的顶点
的顶点 与点A重合,并绕点A按逆时针方向旋转,使点D,A(
与点A重合,并绕点A按逆时针方向旋转,使点D,A( ),B在同一条直线上,如图2所示,观察图2可知:旋转角
),B在同一条直线上,如图2所示,观察图2可知:旋转角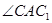 = ° ,与BC相等的线段是 。
= ° ,与BC相等的线段是 。

 ,连接
,连接 ,求
,求 的度数。
的度数。查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
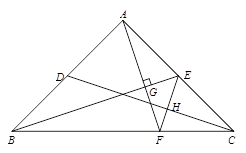
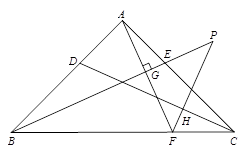
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
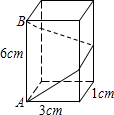
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com