
ЁОЬтФПЁПШчЭМЃЌХзЮяЯпyЃНЉ![]() x2+
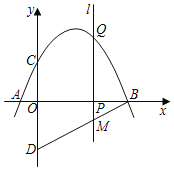
x2+![]() x+2гыxжсНЛгкЕуAЃЌЕуBЃЌгыyжсНЛгкЕуCЃЌЕуDгыЕуCЙигкxжсЖдГЦЃЌЕуPЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯп1НЛХзЮяЯпгкЕуQЃЎ
x+2гыxжсНЛгкЕуAЃЌЕуBЃЌгыyжсНЛгкЕуCЃЌЕуDгыЕуCЙигкxжсЖдГЦЃЌЕуPЪЧxжсЩЯЕФвЛИіЖЏЕуЃЌЩшЕуPЕФзјБъЮЊЃЈmЃЌ0ЃЉЃЌЙ§ЕуPзїxжсЕФДЙЯп1НЛХзЮяЯпгкЕуQЃЎ
ЃЈ1ЃЉЧѓЕуAЁЂЕуBЁЂЕуCЕФзјБъЃЛ
ЃЈ2ЃЉЕБЕуPдкЯпЖЮOBЩЯдЫЖЏЪБЃЌжБЯп1НЛжБЯпBDгкЕуMЃЌЪдЬНОПmЮЊКЮжЕЪБЃЌЫФБпаЮCQMDЪЧЦНааЫФБпаЮЃЛ
ЃЈ3ЃЉЕуPдкЯпЖЮABЩЯдЫЖЏЙ§ГЬжаЃЌЪЧЗёДцдкЕуQЃЌЪЙЕУвдЕуBЁЂQЁЂMЮЊЖЅЕуЕФШ§НЧаЮгыЁїBODЯрЫЦЃПШєДцдкЃЌЧѓГіЕуQЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЁОД№АИЁПЃЈ1ЃЉAЃЈЉ1ЃЌ0ЃЉЃЌBЃЈ4ЃЌ0ЃЉЃЌCЃЈ0ЃЌ2ЃЉЃЛЃЈ2ЃЉmЃН2ЪБЃЌЫФБпаЮCQMDЪЧЦНааЫФБпаЮЃЛЃЈ3ЃЉДцдкЃЌЕуQЃЈ3ЃЌ2ЃЉЛђЃЈЉ1ЃЌ0ЃЉЃЎ
ЁОНтЮіЁП
ЃЈ1ЃЉСюХзЮяЯпЙиЯЕЪНжаЕФxЃН0ЛђyЃН0ЃЌЗжБ№ЧѓГіyЁЂxЕФжЕЃЌНјЖјЧѓГігыxжсЃЌyжсЕФНЛЕузјБъЃЛ
ЃЈ2ЃЉгУmБэЪОГіЕуQЃЌMЕФзнзјБъЃЌНјЖјБэЪОQMЕФГЄЃЌЪЙCDЃНQMЃЌМДПЩЧѓГіmЕФжЕЃЛ
ЃЈ3ЃЉЗжШ§жжЧщПіНјааНтД№ЃЌМДЂйЁЯMBQЃН90ЁуЃЌЂкЁЯMQBЃН90ЁуЃЌЂлЁЯQMBЃН90ЁуЗжБ№ЛГіЯргІЭМаЮНјааНтД№ЃЎ
НтЃКЃЈ1ЃЉХзЮяЯпyЃНЉ![]() x2+
x2+![]() x+2ЃЌЕБxЃН0ЪБЃЌyЃН2ЃЌвђДЫЕуCЃЈ0,2ЃЉЃЌ
x+2ЃЌЕБxЃН0ЪБЃЌyЃН2ЃЌвђДЫЕуCЃЈ0,2ЃЉЃЌ
ЕБyЃН0ЪБЃЌМДЃКЉ![]() x2+
x2+![]() x+2ЃН0ЃЌНтЕУx1ЃН4ЃЌx2ЃНЉ1ЃЌвђДЫЕуAЃЈЉ1,0ЃЉЃЌBЃЈ4,0ЃЉЃЌ
x+2ЃН0ЃЌНтЕУx1ЃН4ЃЌx2ЃНЉ1ЃЌвђДЫЕуAЃЈЉ1,0ЃЉЃЌBЃЈ4,0ЃЉЃЌ
ЙЪЃКAЃЈЉ1,0ЃЉЃЌBЃЈ4,0ЃЉЃЌCЃЈ0,2ЃЉЃЛ
ЃЈ2ЃЉЁпЕуDгыЕуCЙигкxжсЖдГЦЃЌЁрЕуDЃЈ0,Љ2ЃЉЃЌCDЃН4ЃЌ
ЩшжБЯпBDЕФЙиЯЕЪНЮЊyЃНkx+bЃЌАбDЃЈ0,Љ2ЃЉЃЌBЃЈ4,0ЃЉДњШыЕУЃЌ
![]() ЃЌНтЕУЃЌkЃН
ЃЌНтЕУЃЌkЃН![]() ЃЌbЃНЉ2ЃЌ
ЃЌbЃНЉ2ЃЌ
ЁржБЯпBDЕФЙиЯЕЪНЮЊyЃН![]() xЉ2
xЉ2
ЩшMЃЈm,![]() mЉ2ЃЉЃЌQЃЈm,Љ
mЉ2ЃЉЃЌQЃЈm,Љ![]() m2+
m2+![]() m+2ЃЉЃЌ
m+2ЃЉЃЌ
ЁрQMЃНЉ![]() m2+
m2+![]() m+2Љ
m+2Љ![]() m+2ЃЉЃНЉ
m+2ЃЉЃНЉ![]() m2+m+4ЃЌ
m2+m+4ЃЌ
ЕБQMЃНCDЪБЃЌЫФБпаЮCQMDЪЧЦНааЫФБпаЮЃЛ
ЁрЉ![]() m2+m+4ЃН4ЃЌ
m2+m+4ЃН4ЃЌ
НтЕУm1ЃН0ЃЈЩсШЅЃЉЃЌm2ЃН2ЃЌ
Д№ЃКmЃН2ЪБЃЌЫФБпаЮCQMDЪЧЦНааЫФБпаЮЃЛ
ЃЈ3ЃЉдкRtЁїBODжаЃЌODЃН2ЃЌOBЃН4ЃЌвђДЫOBЃН2ODЃЌ
ЂйШєЁЯMBQЃН90ЁуЪБЃЌШчЭМ1ЫљЪОЃЌ
ЕБЁїQBMЁзЁїBODЪБЃЌQPЃН2PBЃЌ
ЩшЕуPЕФКсзјБъЮЊxЃЌдђQPЃНЉ![]() x2+
x2+![]() x+2ЃЌPBЃН4ЉxЃЌ
x+2ЃЌPBЃН4ЉxЃЌ
гкЪЧЉ![]() x2+
x2+![]() x+2ЃН2ЃЈ4ЉxЃЉЃЌ
x+2ЃН2ЃЈ4ЉxЃЉЃЌ
НтЕУЃЌx1ЃН3ЃЌx2ЃН4ЃЈЩсШЅЃЉЃЌ
ЕБxЃН3ЪБЃЌPBЃН4Љ3ЃН1ЃЌ
ЁрPQЃН2PBЃН2ЃЌ
ЁрЕуQЕФзјБъЮЊЃЈ3ЃЌ2ЃЉЃЛ
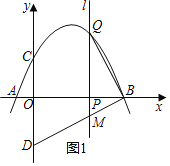
ЂкШєЁЯMQBЃН90ЁуЪБЃЌШчЭМ2ЫљЪОЃЌДЫЪБЕуPЁЂQгыЕуAжиКЯЃЌ
ЁрQЃЈЉ1ЃЌ0ЃЉЃЛ
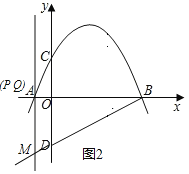
ЂлгЩгкЕуMдкжБЯпBDЩЯЃЌвђДЫЁЯQMBЁй90ЁуЃЌетжжЧщПіВЛДцдкЁїQBMЁзЁїBODЃЎ
злЩЯЫљЪіЃЌЕуPдкЯпЖЮABЩЯдЫЖЏЙ§ГЬжаЃЌДцдкЕуQЃЌЪЙЕУвдЕуBЁЂQЁЂMЮЊЖЅЕуЕФШ§НЧаЮгыЁїBODЯрЫЦЃЌ
ЕуQЃЈ3ЃЌ2ЃЉЛђЃЈЉ1ЃЌ0ЃЉЃЎ


 ЪжРЪжШЋгХСЗПМОэЯЕСаД№АИ
ЪжРЪжШЋгХСЗПМОэЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЩЬЕъНЋУПМўНјМлЮЊ80дЊЕФФГжжЩЬЕъАДУПМў110дЊГіЪлЃЌУПЬьПЩЪлГі100МўЃЎИУЩЬЕъЯыЭЈЙ§НЕЕЭЪлМлЁЂдіМгЯњЪлСПЕФЗНЗЈРДЬсИпРћШѓЃЎОЪаГЁЕїВщЃЌЗЂЯжетжжЩЬЦЗУПМўУПНЕМл5дЊЃЌУПЬьЕФЯњЪлСППЩдіМг50МўЃЎЩшЩЬЦЗНЕМлxдЊЃЌУПЬьЯњЪлИУЩЬЦЗЛёЕУЕФРћШѓЮЊyдЊЃЎ
ЃЈ1ЃЉЧѓyЃЈдЊЃЉЙигкxЃЈдЊЃЉЕФКЏЪ§ЙиЯЕЪНЃЌВЂаДГіxЕФШЁжЕЗЖЮЇЃЎ
ЃЈ2ЃЉЧѓЕБxШЁКЮжЕЪБyзюДѓЃПВЂЧѓГіyЕФзюДѓжЕЃЎ
ЃЈ3ЃЉШєвЊЪЧУПЬьЯњЪлРћШѓЮЊ3750дЊЃЌЧвОЁПЩФмзюДѓЕФЯђЙЫПЭШУРћЃЌгІНЋИУЩЬЦЗНЕМлЖрЩйдЊЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
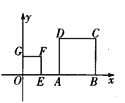
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮOEFGКЭе§ЗНаЮABCDЪЧЮЛЫЦЭМаЮЃЌЕуFЕФзјБъЮЊ(1ЃЌ1)ЃЌЕуCЕФзјБъЮЊ(4ЃЌ2)ЃЌдђетСНИіе§ЗНаЮЮЛЫЦжааФЕФзјБъЪЧ______
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌХзЮяЯп![]() ЕФЖдГЦжсЮЊ
ЕФЖдГЦжсЮЊ![]() ЃЌЧвЙ§Еу
ЃЌЧвЙ§Еу![]() ЃЌгаЯТСаНсТлЃКЂй
ЃЌгаЯТСаНсТлЃКЂй![]() ЃЛЂк
ЃЛЂк![]() ЃЛЂл
ЃЛЂл![]() ЃЛЂм
ЃЛЂм![]() ЃЛЦфжаЫљгае§ШЗЕФНсТлЪЧЃЈЬюађКХЃЉЃК______________ЃЎ
ЃЛЦфжаЫљгае§ШЗЕФНсТлЪЧЃЈЬюађКХЃЉЃК______________ЃЎ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
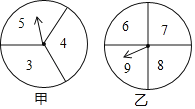
ЁОЬтФПЁПдквЛДЮЪ§бЇаЫШЄаЁзщЛюЖЏжаЃЌбєЙтКЭРжЙлСНЮЛЭЌбЇЩшМЦСЫШчЭМЫљЪОЕФСНИізЊХЬзігЮЯЗЃЈУПИізЊХЬБЛЗжГЩУцЛ§ЯрЕШЕФМИИіЩШаЮЃЌВЂдкУПИіЩШаЮЧјгђФкБъЩЯЪ§зжЃЉЃЎгЮЯЗЙцдђШчЯТЃКСНШЫЗжБ№ЭЌЪБзЊЖЏМзЁЂввзЊХЬЃЌзЊХЬЭЃжЙКѓЃЌШєжИеыЫљжИЧјгђФкСНЪ§КЭаЁгк12ЃЌдђбєЙтЛёЪЄЃЌЗДжЎдђРжЙлЛёЪЄЃЈШєжИеыЭЃдкЕШЗжЯпЩЯЃЌжизЊвЛДЮЃЌжБЕНжИеыжИЯђФГвЛЗнФкЮЊжЙЃЉЃЎ
ЃЈ1ЃЉЧыгУСаБэЛђЛЪїзДЭМЕФЗНЗЈБэЪОГіЩЯЪігЮЯЗжаСНЪ§КЭЕФЫљгаПЩФмЕФНсЙћЃЛ
ЃЈ2ЃЉгЮЯЗЖдЫЋЗНЙЋЦНТ№ЃПЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГГЌЪагУ1200дЊЙКНјвЛХњМзЭцОпЃЌгУ800дЊЙКНјвЛХњввЭцОпЃЌЫљЙКМзЭцОпМўЪ§ЪЧввЭцОпМўЪ§ЕФ![]() ЃЌвбжЊМзЭцОпЕФНјЛѕЕЅМлБШввЭцОпЕФНјЛѕЕЅМлЖр1дЊЃЎ
ЃЌвбжЊМзЭцОпЕФНјЛѕЕЅМлБШввЭцОпЕФНјЛѕЕЅМлЖр1дЊЃЎ
ЃЈ1ЃЉЧѓЃКМзЁЂввЭцОпЕФНјЛѕЕЅМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉЭцОпЪлЭъКѓЃЌГЌЪаОіЖЈдйДЮЙКНјМзЁЂввЭцОпЃЈМзЁЂввЭцОпЕФНјЛѕЕЅМлВЛБфЃЉЃЌЙКНјввЭцОпЕФМўЪ§БШМзЭцОпМўЪ§ЕФ2БЖЖр60МўЃЌЧѓЃКИУГЌЪагУВЛГЌЙ§2100дЊзюЖрПЩвдВЩЙКМзЭцОпЖрЩйМўЃП
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЃКШчЭМЃЌЗДБШР§КЏЪ§y= ![]() ЕФЭМЯѓгывЛДЮКЏЪ§y=x+bЕФЭМЯѓНЛ
ЕФЭМЯѓгывЛДЮКЏЪ§y=x+bЕФЭМЯѓНЛ
гкЕуAЃЈ1ЃЌ4ЃЉЁЂЕуBЃЈ-4ЃЌnЃЉЃЎ

ЃЈ1ЃЉЧѓвЛДЮКЏЪ§КЭЗДБШР§КЏЪ§ЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЧѓЁїOABЕФУцЛ§ЃЛ
ЃЈ3ЃЉжБНгаДГівЛДЮКЏЪ§жЕДѓгкЗДБШР§КЏЪ§жЕЕФздБфСПxЕФШЁжЕЗЖЮЇЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
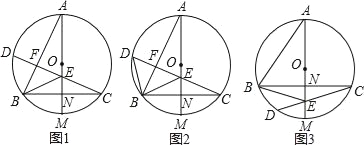
ЁОЬтФПЁПвбжЊAMЪЧЁбOжБОЖЃЌЯвBCЁЭAMЃЌДЙзуЮЊЕуNЃЌЯвCDНЛAMгкЕуEЃЌСЌАДABКЭBEЃЎ
ЃЈ1ЃЉШчЭМ1ЃЌШєCDЁЭABЃЌДЙзуЮЊЕуFЃЌЧѓжЄЃКЁЯBEDЃН2ЁЯBAMЃЛ
ЃЈ2ЃЉШчЭМ2ЃЌдкЃЈ1ЃЉЕФЬѕМўЯТЃЌСЌНгBDЃЌШєЁЯABEЃНЁЯBDCЃЌЧѓжЄЃКAEЃН2CNЃЛ
ЃЈ3ЃЉШчЭМ3ЃЌABЃНCDЃЌBEЃКCDЃН4ЃК7ЃЌAEЃН11ЃЌЧѓEMЕФГЄЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
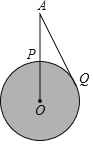
ЁОЬтФПЁПШчЭМЃЌФГКНЬьЗЩЛњдкЕиЧђБэУцЕуPЕФе§ЩЯЗНAДІЃЌДгAДІЙлВтЕНЕиЧђЩЯЕФзюдЖЕуQЃЌМДAQЪЧЁбOЕФЧаЯпЃЌШєЁЯQAPЃНІСЃЌЕиЧђАыОЖЮЊRЃЌ
ЧѓЃК(1)КНЬьЗЩЛњОрЕиЧђБэУцЕФзюНќОрРыAPЕФГЄЃЛ
(2)PЁЂQСНЕуМфЕФЕиУцОрРыЃЌМД![]() ЕФГЄЃЎ(зЂЃКБОЬтзюКѓНсЙћОљгУКЌІСЃЌRЕФДњЪ§ЪНБэЪО)
ЕФГЄЃЎ(зЂЃКБОЬтзюКѓНсЙћОљгУКЌІСЃЌRЕФДњЪ§ЪНБэЪО)
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com