
【题目】如图,已知一次函数y=x﹣2与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积.
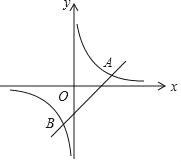
【答案】(1)A(3,1)、B(﹣1,﹣3)(2)x<﹣1或0<x<3(3)4
【解析】试题分析:(1)联立方程组,解方程组即可得到A、B的坐标;
(2)根据图像确定一次函数的图像在反比例函数的图像上的x范围即可;
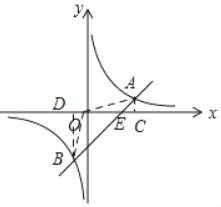
(3)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,构造三角形,求三角形的面积和即可.
试题解析:(1)联立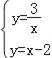
解得:![]() 或
或![]()
∴A(3,1)、B(﹣1,﹣3)
(2)x的取值范围为:x<﹣1或0<x<3
(3)过点A作AC⊥x轴于点C,过点B作BD⊥x轴于点D,
令y=0代入y=x﹣2
∴x=2,
∴E(2,0)
∴OE=2
∵A(3,1)、B(﹣1,﹣3)
∴AC=1,BD=3,
∴△AOE的面积为:![]() ACOE=1,
ACOE=1,
△BOE的面积为:![]() BDOE=3,
BDOE=3,
∴△ABC的面积为:1+3=4,


 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案科目:初中数学 来源: 题型:
【题目】九(1)班数学兴趣小组经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销售量的相关信息如下表:
时间x(天) | 1≤x<50 | 50≤x≤90 |
售价(元/件) | x+40 | 90 |
每天销量(件) | 200-2x | |
已知该商品的进价为每件30元,设销售该商品的每天利润为y元[
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
(3)该商品在销售过程中,共有多少天每天销售利润不低于4800元?请直接写出结果.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某公司计划在某地区销售一款5G产品,根据市场分析,该产品的销售价格将随销售周期的变化而变化.该产品在第x周(x为正整数,且1≤x≤8)个销售周期的销售价格为y元,y与x之间满足如图所示的一次函数.
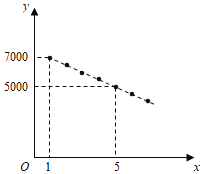
(1)求y与x之间的函数关系;
(2)产品在第x个销售周期的销售数量为p万台,p与x之间满足:![]() .已知在某个销售周期的销售收入是16000万元,求此时该产品的销售价格是多少元?
.已知在某个销售周期的销售收入是16000万元,求此时该产品的销售价格是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
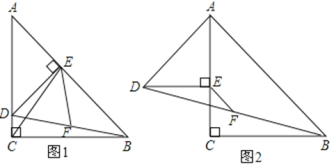
【题目】在△ABC和△ADE中AC=BC,AE=DE , ∠ACB=∠AED=90° , 点E在AB上,F是线段BD的中点,连接CE、FE.
(1)若AD=3![]() ,BE=4 ,求EF的长
,BE=4 ,求EF的长
(2)求证:CE=![]() EF
EF
(3)将图1中的△ADE绕点A顺时针旋转,使△AED的一边AE恰好与△ABC的边AC在同一条直线上(如图2),连接BD,取BD的中点F,问(2)中的结论是否仍然成立,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△ABO的顶点A是反比例函数y=![]() 与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=
与一次函数y=﹣x﹣(k+1)的图象在第二象限的交点,AB⊥x轴于B,且S△ABO=![]() .
.
(1)直接写出这两个函数的关系式;
(2)求△AOC的面积;
(3)根据图象直接写出:当x为何值时,反比例函数的值小于一次函数的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
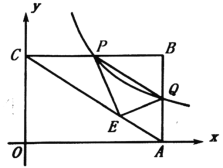
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 、
、![]() 分别在轴和y轴上,
分别在轴和y轴上,![]() ,
,![]() ,点Q是
,点Q是![]() 边上一个动点,过点Q的反比例函数
边上一个动点,过点Q的反比例函数![]() 与
与![]() 边交于点P.若将
边交于点P.若将![]() 沿
沿![]() 折叠,点B的对应点E恰好落在对角线
折叠,点B的对应点E恰好落在对角线![]() 上,则此时反比例函数的解析式是_______.
上,则此时反比例函数的解析式是_______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴交于A、B两点,与轴交于点
与x轴交于A、B两点,与轴交于点![]() ,连接
,连接![]() 、
、![]() .
.
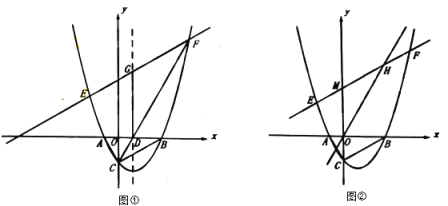
(1)求抛物线的函数表达式;
(2)抛物线的对称轴与x轴交于点D,连接![]() ,点E为第三象限抛物线上的一动点,
,点E为第三象限抛物线上的一动点,![]() ,直线
,直线![]() 与抛物线交于点F,设直线
与抛物线交于点F,设直线![]() 的表达式为
的表达式为![]() .
.
①如图①,直线![]() 与抛物线对称轴交于点G,若
与抛物线对称轴交于点G,若![]() ,求k、b的值;
,求k、b的值;
②如图②,直线![]() 与y轴交于点M,与直线
与y轴交于点M,与直线![]() 交于点H,若
交于点H,若![]() ,求b的值.
,求b的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
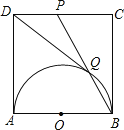
【题目】如图,正方形ABCD边长为1,以AB为直径作半圆,点P是CD中点,BP与半圆交于点Q,连接![]() 给出如下结论:
给出如下结论:![]() ;
;![]() ;
;![]() ;
;![]() 其中正确的结论是______
其中正确的结论是______![]() 填写序号
填写序号![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为了测量一个铁球的直径,将该铁球放入工件槽内,测得的有关数据如图所示(单位:cm),则该铁球的直径为( )
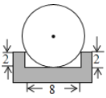
A.12 cmB.10 cmC.8 cmD.6 cm
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com