
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与x轴交于A、B两点,与轴交于点
与x轴交于A、B两点,与轴交于点![]() ,连接
,连接![]() 、
、![]() .
.
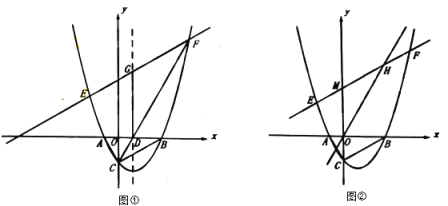
(1)求抛物线的函数表达式;
(2)抛物线的对称轴与x轴交于点D,连接![]() ,点E为第三象限抛物线上的一动点,
,点E为第三象限抛物线上的一动点,![]() ,直线
,直线![]() 与抛物线交于点F,设直线
与抛物线交于点F,设直线![]() 的表达式为
的表达式为![]() .
.
①如图①,直线![]() 与抛物线对称轴交于点G,若
与抛物线对称轴交于点G,若![]() ,求k、b的值;
,求k、b的值;
②如图②,直线![]() 与y轴交于点M,与直线
与y轴交于点M,与直线![]() 交于点H,若
交于点H,若![]() ,求b的值.
,求b的值.
【答案】(1)![]() ;(2)①k=
;(2)①k=![]() ,b=
,b=![]() ,②
,②![]() .
.
【解析】
(1)把![]() 代入
代入![]() ,求出a的值,即可;
,求出a的值,即可;
(2)①由![]() ,DG=FG,由
,DG=FG,由![]() ,∠GMD=∠OBC=30°,过点G作GN∥x轴,过点F作FN∥y轴,交于点N,交x轴于点H,则∠FGN=30°,设DG=FG=m,得:点F坐标是:(1+
,∠GMD=∠OBC=30°,过点G作GN∥x轴,过点F作FN∥y轴,交于点N,交x轴于点H,则∠FGN=30°,设DG=FG=m,得:点F坐标是:(1+![]() ,
,![]() ),代入二次函数得解析式,可得:点F坐标是:(5,
),代入二次函数得解析式,可得:点F坐标是:(5,![]() ),由∠GMD=30°和待定系数法,分别可得k,b的值;
),由∠GMD=30°和待定系数法,分别可得k,b的值;
②由直线![]() 与y轴交于点M,与直线
与y轴交于点M,与直线![]() 交于点H,
交于点H,![]() ,可得:
,可得:![]() ,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,MH=MO=b,作EG⊥y轴,FN⊥y轴,则,ME=
,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,MH=MO=b,作EG⊥y轴,FN⊥y轴,则,ME=![]() EG,MF=
EG,MF=![]() FN,设点E,F的很坐标分别是:
FN,设点E,F的很坐标分别是:![]() ,
,![]() ,由
,由![]() ,得到关于b的方程,即可求解.
,得到关于b的方程,即可求解.
(1)把![]() 代入
代入![]() 得:
得:![]() ,解得:
,解得:![]() ,
,
∴抛物线的函数表达式为:![]() ;
;
(2)① 由第(1)题,可知:A(-1,0),B(3,0),![]() ,
,
∴OB=3,OC=![]() ,BC=
,BC=![]() =
=![]() ,
,
∴∠OBC=30°,
∵抛物线的对称轴与x轴交于点D,
∴D坐标为(1,0),即OD=1,BD=2,
∴CD=![]() ,
,
∴BD=CD,
∵![]() ,
,
∴DG=FG,
∵![]() ,
,
∴∠GMD=∠OBC=30°,
过点G作GN∥x轴,过点F作FN∥y轴,交于点N,交x轴于点H,则∠FGN=30°,如图①,
设DG=FG=m,则![]() ,
,![]() ,
,![]() ,
,
∴FH=FN+NH=![]() ,OH=OD+DH=1+
,OH=OD+DH=1+![]() ,
,
∴点F坐标是:(1+![]() ,
,![]() ),
),
∴![]() ,解得:
,解得:![]() ,
,![]() (舍)
(舍)
∴点F坐标是:(5,![]() ),
),
∵∠GMD=30°,可设直线![]() 的表达式为
的表达式为![]() ,
,
把(5,![]() )代入
)代入![]() ,得:
,得:![]() ,解得:b=
,解得:b=![]() ,
,
∴直线![]() 的表达式为:
的表达式为:![]() ,即:k=
,即:k=![]() ,b=
,b=![]() .
.
②∵直线![]() 与y轴交于点M,与直线
与y轴交于点M,与直线![]() 交于点H,
交于点H,![]() ,
,
∴![]() ,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,
,∠EMO=∠OCB=60°,∠HOB=60°,∠MOH=∠MHO=30°,
∴MH=MO=b,
作EG⊥y轴,FN⊥y轴,则,ME=![]() EG,MF=
EG,MF=![]() FN,
FN,
设点E,F的很坐标分别是:![]() ,
,![]()
联立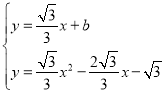 ,得:
,得:![]() ,
,
化简得:![]() ,
,
∴![]() +
+![]() =3,
=3,![]()
![]() =
=![]() ,
,
∵![]() ,
,
∴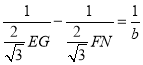 ,即:
,即: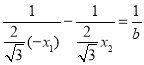 ,
,
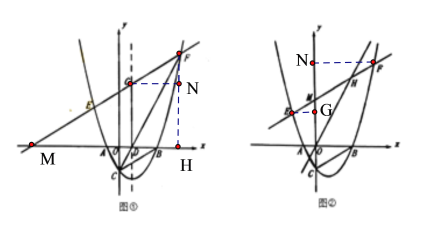
化简得: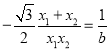 ,
,
∴![]() ,解得:b=
,解得:b=![]()


 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
【题目】已知,在△PAB中,PA=PB,经过A、B作⊙O.

(1)如图1,连接PO,求证:PO平分∠APB;
(2)如图2,点P在⊙O上,PA:AB=![]() :2,E是⊙O上一点,连接AE、BE.求tan∠AEB的值;
:2,E是⊙O上一点,连接AE、BE.求tan∠AEB的值;
(3)如图3,在(2)的条件下,AE经过圆心O,AE交PB于点F,过F作FG⊥BE于点G,EF+BG=14,求线段OF的长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() 的对称轴为
的对称轴为![]() ,与
,与![]() 轴的一个交点在
轴的一个交点在![]() 和
和![]() 之间,其部分图象如图所示,则下列结论:
之间,其部分图象如图所示,则下列结论:
![]() ;
;
![]() ;
;
![]() 点
点![]() 、
、![]() 、
、![]() 是该抛物线上的点,则
是该抛物线上的点,则![]() ;
;
![]() ;
;
![]() (
(![]() 为任意实数).
为任意实数).
其中正确结论的个数是( )

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
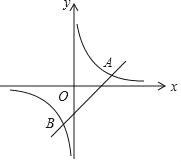
【题目】如图,已知一次函数y=x﹣2与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
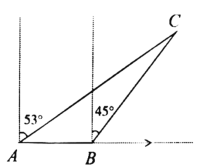
【题目】如图,渔船跟踪鱼群由西向东航行,到达A处时,测得小岛C位于它的北偏东53°方向,再航行![]() 后达到B处(
后达到B处(![]() ),测得小岛C位于它的北偏东45°方向.小岛C的周围
),测得小岛C位于它的北偏东45°方向.小岛C的周围![]() 内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
内有暗礁,如果渔船不改变航向继续向东航行,请你通过计算说明渔船有无触礁的危险?
(参考数据:![]() ,
,![]() ,
,![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳著名“网红打卡地”东部华侨城在2018年春节长假期间,接待游客达20万人次,预计在2020年五一长假期间,接待游客奖达28.8万人次.
一家特色小面店希望在五一长期限期间获得好的收益,经测算知,该小面成本价为每碗6元,借鉴经验:若每碗卖25元,平均每天将销售3000碗,若价格每降低1元,则平均每天多销售30碗.
(1)求出2018至2020年五一长假期间游客人次的年平均增长率;
(2)为了更好地维护深圳城市形象,店家规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天利润6300元?
查看答案和解析>>
科目:初中数学 来源: 题型:
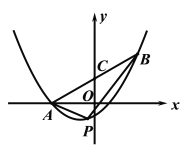
【题目】如图,抛物线![]() 过点
过点![]() 和点
和点![]() ,连结AB交y轴于点C.
,连结AB交y轴于点C.
(1)求抛物线的函数解析式;
(2)点P在线段AB下方的抛物线上运动,连结AP,BP. 设点P的横坐标为m,△ABP的面积为s.
①求s与m的函数关系式;
②当s取最大值时,抛物线上是否存在点Q,使得S△ACQ=s. 若存在,求点Q的坐标;若不存在,说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系xOy中,抛物线y=ax2-4ax+c(a≠0)与y轴交于点A,将点A向右平移2个单位长度,得到点B.直线![]() 与x轴,y轴分别交于点C,D.
与x轴,y轴分别交于点C,D.
(1)求抛物线的对称轴.
(2)若点A与点D关于x轴对称.
①求点B的坐标.
②若抛物线与线段BC恰有一个公共点,结合函数图象,求a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com