
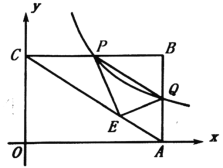
【题目】如图,在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 、
、![]() 分别在轴和y轴上,
分别在轴和y轴上,![]() ,
,![]() ,点Q是
,点Q是![]() 边上一个动点,过点Q的反比例函数
边上一个动点,过点Q的反比例函数![]() 与
与![]() 边交于点P.若将
边交于点P.若将![]() 沿
沿![]() 折叠,点B的对应点E恰好落在对角线
折叠,点B的对应点E恰好落在对角线![]() 上,则此时反比例函数的解析式是_______.
上,则此时反比例函数的解析式是_______.
【答案】![]()
【解析】
由题意得:直线AC的函数解析式为:y=![]() x+4,设点E坐标是:(x,
x+4,设点E坐标是:(x,![]() x+4),作EM⊥BC,EN⊥AB,则ME=4-(
x+4),作EM⊥BC,EN⊥AB,则ME=4-(![]() x+4)=
x+4)= ![]() x,NE=6-x,易证:PME~QNE,进而得到:
x,NE=6-x,易证:PME~QNE,进而得到: ,求出点E坐标是:(
,求出点E坐标是:(![]() ,
,![]() ),在RtPME中,PM2+ME2=PE2,列出方程,即可求出k得值,进而得到答案.
),在RtPME中,PM2+ME2=PE2,列出方程,即可求出k得值,进而得到答案.
∵在平面直角坐标系![]() 中,矩形
中,矩形![]() 的边
的边![]() 、
、![]() 分别在x轴和y轴上,
分别在x轴和y轴上,![]() ,
,![]() ,
,
∴点A坐标是:(6,0),点C坐标是:(0,4),
设直线AC的函数解析式为:y=kx+b,把(6,0),(0,4),代入得:![]()
解得: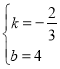 ,
,
∴直线AC的函数解析式为:y=![]() x+4,
x+4,
∵点E恰好落在对角线![]() 上,
上,
设点E坐标是:(x,![]() x+4),作EM⊥BC,EN⊥AB,则ME=4-(
x+4),作EM⊥BC,EN⊥AB,则ME=4-(![]() x+4)=
x+4)= ![]() x,NE=6-x,∠PEM=∠QEN,∠PME=∠QNE=90°,
x,NE=6-x,∠PEM=∠QEN,∠PME=∠QNE=90°,
∴PME~
∴![]() ,
,
∵点Q是![]() 边上一个动点,过点Q的反比例函数
边上一个动点,过点Q的反比例函数![]() 与
与![]() 边交于点P,
边交于点P,
∴Q(6,![]() ),P(
),P(![]() ,4),
,4),
∵![]() 沿
沿![]() 折叠得到
折叠得到![]()
∴PB=PE=6-![]() ,BQ=EQ=4-
,BQ=EQ=4-![]() ,
,
∴ ,即:
,即: ,解得:x=
,解得:x=![]() ,
,
∴点E坐标是:(![]() ,
,![]() )
)
∵在RtPME中,PM2+ME2=PE2,
∴![]() ,解得:k=
,解得:k=![]() ,
,
∴反比例函数的解析式为:![]() ,
,
故答案是:![]() .
.



 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】2018年非洲猪瘟疫情暴发后,专家预测,2019年我市猪肉售价将逐月上涨,每千克猪肉的售价y1(元)与月份x(1≤x≤12,且x为整数)之间满足一次函数关系,如下表所示.每千克猪肉的成本y2(元)与月份x(1≤x≤12,且x为整数)之间满足二次函数关系,且3月份每千克猪肉的成本全年最低,为9元,如图所示.
月份x | … | 3 | 4 | 5 | 6 | … |
售价y1/元 | … | 12 | 14 | 16 | 18 | … |

(1)求y1与x之间的函数关系式.
(2)求y2与x之间的函数关系式.
(3)设销售每千克猪肉所获得的利润为w(元),求w与x之间的函数关系式,哪个月份销售每千克猪肉所第获得的利润最大?最大利润是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知O是坐标原点,B、C两点的坐标分别为(3,-1)、(2,1).
(1)以O点为位似中心在y轴的左侧将△OBC放大到两倍(即新图与原图的相似比为2),画出图形;
(2)B点的对应点B′的坐标是 ;C点的对应点C′的坐标是 ;
(3)在BC上有一点P(x,y),按(1)的方式得到的对应点P′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】现将标有数字1、2、3、4的四张卡片洗匀后,背面朝上放在桌子上,所有卡片的形状、大小都完全相同.现随机从中抽取一张卡片将其上面的数字作为十位上的数,然后放回洗匀,再随机抽取一张卡片,将其上面的数字作为个位上的数,组成两位数.
(1)请用列表或画树状图的方法表示出所有可能出现的结果:
(2)求这个两位数恰好能被3整除的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
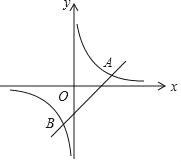
【题目】如图,已知一次函数y=x﹣2与反比例函数y=![]() 的图象交于A、B两点.
的图象交于A、B两点.
(1)求A、B两点的坐标;
(2)观察图象,直接写出一次函数值小于反比例函数值的x的取值范围;
(3)坐标原点为O,求△AOB的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商店购进一批单价为8元的商品,经调研发现,这种商品每天的销售量y(件)是关于销售单价x(元)的一次函数,其关系如下表:
x(元) | 10 | 11 | 12 | 13 | 14 |
y(件) | 100 | 90 | 80 | 70 | 60 |
(1)求y与x之间的关系式;
(2)设商店每天销售利润为w(元),求出w与x之间的关系式,并求出每天销售单价定为多少时利润最大?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】深圳著名“网红打卡地”东部华侨城在2018年春节长假期间,接待游客达20万人次,预计在2020年五一长假期间,接待游客奖达28.8万人次.
一家特色小面店希望在五一长期限期间获得好的收益,经测算知,该小面成本价为每碗6元,借鉴经验:若每碗卖25元,平均每天将销售3000碗,若价格每降低1元,则平均每天多销售30碗.
(1)求出2018至2020年五一长假期间游客人次的年平均增长率;
(2)为了更好地维护深圳城市形象,店家规定每碗售价不得超过20元,则当每碗售价定为多少元时,店家才能实现每天利润6300元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,抛物线y=ax2+bx+c与坐标轴分别交于点A(0,6),B(6,0),C(﹣2,0),点P是线段AB上方抛物线上的一个动点.
(1)求抛物线的解析式;
(2)当点P运动到什么位置时,△PAB的面积有最大值?
(3)过点P作x轴的垂线,交线段AB于点D,再过点P做PE∥x轴交抛物线于点E,连结DE,请问是否存在点P使△PDE为等腰直角三角形?若存在,求出点P的坐标;若不存在,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下面是小石设计的“过圆上一点作圆的切线”的尺规作图的过程.
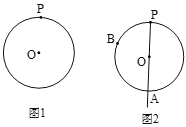
已知:如图1,![]() 及
及![]() 上一点P.
上一点P.
求作:直线PQ,使得PQ与![]() 相切.
相切.
作法:如图2,
①连接PO并延长交![]() 于点A;
于点A;
②在![]() 上任取一点B(点P,A除外),以点B为圆心,BP长为半径作
上任取一点B(点P,A除外),以点B为圆心,BP长为半径作![]() ,与射线PO的另一个交点为C.
,与射线PO的另一个交点为C.
③连接CB并延长交![]() 于点Q.
于点Q.
④作直线PQ;
所以直线PQ就是所求作的直线.
根据小石设计的尺规作图的过程.
(1)使用直尺和圆规,补全图形:(保留作图痕迹)
(2)完成下面的证明.
证明:∵CQ是的![]() 直径,
直径,
∴![]() ________
________![]() (________________)(填推理的依据)
(________________)(填推理的依据)
∴![]() .
.
又∵OP是![]() 的半径,
的半径,
∴PQ是![]() 的切线(________________)(填推理的依据)
的切线(________________)(填推理的依据)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com