
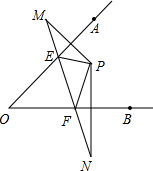
 如图,点P在∠AOB的内部,作点P关于直线OA、OB的对称点M,N,连结MN交OA、OB于点E、F.
如图,点P在∠AOB的内部,作点P关于直线OA、OB的对称点M,N,连结MN交OA、OB于点E、F.分析 (1)根据轴对称的性质可知:EP=EM,PF=FN,所以线段MN的长=△PEF的周长;
(2)结合线段垂直平分线的性质和等腰三角形的性质推知OP=OM,∠MOA=∠AOP,同理,∠BOP=∠BON,则∠MON=2∠AOB=90°.
解答 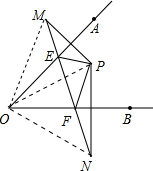 解:(1)根据题意,EP=EM,PF=FN,
解:(1)根据题意,EP=EM,PF=FN,
∴MN=ME+EF+FN=PE+EF+PF=△PEF的周长,
∴MN=20cm;
(2)如图,连接OP、OM、ON.
∵OA垂直平分MP,
∴OP=OM,
∴∠MOA=∠AOP,
同理,∠BOP=∠BON,
∵∠AOB=∠AOP+∠BOP=45°.
∴∠MON=2∠AOB=90°.
点评 本题考查轴对称的性质与运用,对应点的连线与对称轴的位置关系是互相垂直,对应点所连的线段被对称轴垂直平分,对称轴上的任何一点到两个对应点之间的距离相等,对应的角、线段都相等.


 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com