
���� ��1������·�̳����ٶȵó��ס��ҵ��ٶȼ��ɣ� ����·�̳��Լ���ʱ�ٶ���÷���ʱ���ټ��ϴ�A�ص�B�ص�ʱ�伴�ɣ�
��2�������xСʱ����������������������·�̺�Ϊ100km�г����̽�ɣ�
��3�������aСʱ���������30ǧ�ף���������ǰ����������A������ǰ������A�����Һ���������г����̽�ɣ�
��� �⣺��1���ҵ��ٶ���100��5=20km/h���״�A�ص�B�ص��ٶ���100��2=50 km/h�����ڳ���2+100�£�50+30��=3.25Сʱ����A�أ�
��2�������xСʱ�����������������
50x+20x=100
��ã�x=$\frac{10}{7}$��
�𣺳���$\frac{10}{7}$Сʱ����������
��3�������aСʱ���������30ǧ�ף��������
50a+20a=100-30��50a+20a=100+30��20a-��50+30����a-2��=30��50+30����a-2��-20a=30��
��ã�a=1��a=$\frac{13}{7}$��a=$\frac{13}{6}$��a=$\frac{19}{6}$
�𣺳���1��$\frac{13}{7}$��$\frac{13}{6}$��$\frac{19}{6}$Сʱ���������30ǧ�ף�
���� ���⿼��һԪһ�η��̵�ʵ�����ã������г������еĻ���������ϵ�ǽ������Ĺؼ���ע���������˼�������


 ���Ͱ�ͨ��ĩ���ϵ�д�
���Ͱ�ͨ��ĩ���ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
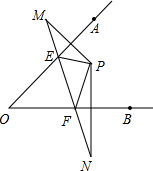 ��ͼ����P�ڡ�AOB���ڲ�������P����ֱ��OA��OB�ĶԳƵ�M��N������MN��OA��OB�ڵ�E��F��
��ͼ����P�ڡ�AOB���ڲ�������P����ֱ��OA��OB�ĶԳƵ�M��N������MN��OA��OB�ڵ�E��F���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com