
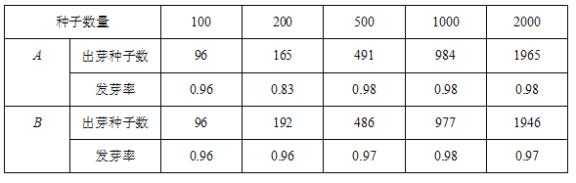
【题目】农科院新培育岀A、B两种新麦种,为了了解它们的发芽情况,在推广前做了五次发芽实验,每次随机各自取相同种子数,在相同的培育环境中分别实验,实验情况记录如下:
下面有三个推断:
①在同样的地质环境下播种,A种子的出芽率可能会高于B种子.
②当实验种子数里为100时,两种种子的发芽率均为0.96所以他发芽的概率一样;
③随着实验种子数量的增加,A种子出芽率在0.98附近摆动,显示出一定的稳定性,可以估计A种子出芽的概率是0.98;其中不合理的是_____(只填序号)
【答案】②.
【解析】
大量重复实验时,事件发生的频率在某个固定位置左右摆动,并且摆动的幅度越来越小,根据这个频率稳定性定理,可以用频率的集中趋势来估计概率,这个固定的近似值就是这个事件的概率,据此解答可得.
①在同样的地质环境下播种,A种子的出芽率约为0.98、B种子的出芽率约为0.97,可能会高于B种子,故①合理;
②在大量重复试验时,随着试验次数的增加,可以用一个事件出现的概率估计它的概率,实验种子数量为100,数量太少,不可用于估计概率,故②推断不合理.
③随着实验种子数量的增加,A种子出芽率在0.98附近摆动,显示出一定的稳定性,可以估计A种子出芽的概率是0.98,故推断合理.
故答案为:②.


 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案科目:初中数学 来源: 题型:
【题目】已知二次函数y=x2﹣(2m+1)x﹣3m.
(1)若m=2,写出该函数的表达式,并求出函数图象的对称轴.
(2)已知点P(m,y1),Q(m+4,y2)在该函数图象上,试比较y1,y2的大小.
(3)对于此函数,在﹣1≤x≤1的范围内至少有x值使得y≥0,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】请用学过的方法研究一类新函数![]() (
(![]() 为常数,
为常数,![]() )的图象和性质.
)的图象和性质.
(1)在给出的平面直角坐标系中画出函数![]() 的图象;
的图象;
(2)对于函数![]() ,当自变量
,当自变量![]() 的值增大时,函数值
的值增大时,函数值![]() 怎样变化?
怎样变化?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角![]() 中,
中,![]() ,
,![]() ,作
,作![]() 的平分线交
的平分线交![]() 于点
于点![]() ,在
,在![]() 上取点
上取点![]() ,以点
,以点![]() 为圆心经过
为圆心经过![]() 、
、![]() 两点画圆分别与
两点画圆分别与![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() (异于点
(异于点![]() ).
).
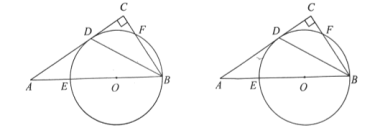
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若点![]() 恰好是
恰好是![]() 的中点,求
的中点,求![]() 的长;
的长;
(3)若![]() 的长为
的长为![]() .
.
①求![]() 的半径长;
的半径长;
②点![]() 关于
关于![]() 轴对称后得到点
轴对称后得到点![]() ,求
,求![]() 与
与![]() 的面积之比.
的面积之比.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知AD为⊙O的直径,BC为⊙O的切线,切点为M,分别过A,D两点作BC的垂线,垂足分别为B,C,AD的延长线与BC相交于点E.
(1)求证:△ABM∽△MCD;
(2)若AD=8,AB=5,求ME的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
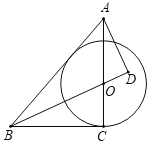
【题目】如图,在△ABC中,O为AC上一点以O为圆心,OC长为半径作圆,与BC相切于点C,过点A作AD⊥BO交BO延长线于点D,且∠AOD=∠BAD.
(1)求证:AB为⊙O的切线;
(2)若BC=6,tan∠ABC![]() ,求OD的长.
,求OD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
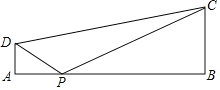
【题目】如图,在四边形ABCD中,∠A=∠B=90°,AB=6,AD=1,BC=2,P为AB边上的动点,当△PAD与△PBC相似时,PA=_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】知,抛物线![]() (a
(a![]() 0)的顶点为A(s,t)(其中s
0)的顶点为A(s,t)(其中s![]() 0) .
0) .
(1)若抛物线经过(2,2)和(-3,37)两点,且s=3.
①求抛物线的解析式;
②若n>3, 设点M(![]() ),N(
),N(![]() )在抛物线上,比较
)在抛物线上,比较![]() ,
,![]() 的大小关系,并说明理由;
的大小关系,并说明理由;
(2)若a=2,c=-2,直线![]() 与抛物线
与抛物线![]() 的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
的交于点P和点Q,点P的横坐标为h,点Q的横坐标为h+3,求出b和h的函数关系式;
(3)若点A在抛物线![]() 上,且2≤s<3时,求a的取值范围.
上,且2≤s<3时,求a的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
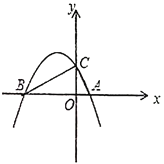
【题目】如图,抛物线![]() 经过点
经过点![]() ,点
,点![]() ,交
,交![]() 轴于点
轴于点![]() ,连接
,连接![]() ,
,![]() .
.
(1)求抛物线的解析式;
(2)点![]() 为抛物线第二象限上一点,满足
为抛物线第二象限上一点,满足![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)将直线![]() 绕点
绕点![]() 顺时针旋转
顺时针旋转![]() ,与抛物线交于另一点
,与抛物线交于另一点![]() ,求点
,求点![]() 的坐标.
的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com