
【题目】将一个直角三角形纸片![]() ,放置在平面直角坐标系中,点
,放置在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]()
(I)过边![]() 上的动点
上的动点![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合)作
重合)作![]() 交
交![]() 于点
于点![]() ,沿着
,沿着![]() 折叠该纸片,点
折叠该纸片,点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处.
处.
①如图,当![]() 为
为![]() 中点时,求
中点时,求![]() 点的坐标;
点的坐标;
②连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 点坐标:
点坐标:
(Ⅱ)![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() 重合),将
重合),将![]() 沿
沿![]() 所在的直线折叠,得到
所在的直线折叠,得到![]() ,连接
,连接![]() ,当
,当![]() 取得最小值时,求
取得最小值时,求![]() 点坐标(直接写出结果即可).
点坐标(直接写出结果即可).
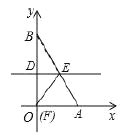
【答案】(I)①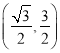 ;②
;②![]() 点坐标为
点坐标为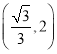 或
或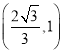 ;(II)
;(II)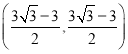
【解析】
(I)①过点E做EH⊥OA ,交OA于点H,由D为OB中点结合DE∥OA,可得出DE为△BOA的中位线,再根据点A、B的坐标即可得出点E的坐标;
②根据折叠的性质结合角的计算可得出∠AEF=60°≠90°,分∠AFE=90°和∠EAF=90°两种情况考虑,利用含30度角的直角三角形以及勾股定理即可求出点E的坐标;
(II)根据三角形的三边关系,找出当点A′在y轴上时,BA′取最小值,根据折叠的性质可得出直线OP的解析式,再根据点A、B的坐标利用待定系数法求出直线AB的解析式,联立两直线解析式成方程组,解之即可得出点P的坐标.
(I)过点E做EH⊥OA ,交OA于点H,
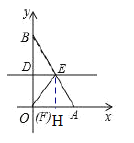
①∵![]() ,
,![]() ,
,
∴![]() .
.
∵![]() 为
为![]() 中点,
中点,
∴D点的坐标为![]() ,
,
∴![]() 为
为![]() 的中位线,
的中位线,
∴点![]() 为线段
为线段![]() 的中点,
的中点,
又∵![]() ,
,
∴EH为![]() 的中位线,
的中位线,
∴点H为线段OA的中点,
∴点H的坐标为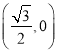 ,
,
∴点![]() 的坐标为
的坐标为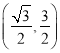 .
.
②∵点![]() ,点
,点![]() ,
,
∴![]() ,OB=3
,OB=3
∴![]() ,
,
∴∠B=30°,
由折叠可知:![]() .
.
∴![]() ,
,![]()
∴![]() .
.
∵![]() 是直角三角形,
是直角三角形,
∴![]() 或
或![]()
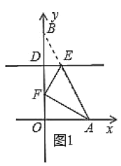
(i)当![]() 时,如图1所示
时,如图1所示
![]() .
.
在![]() 中,
中,![]() ,
,![]()
∴![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
,![]() .
.
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
∵![]() .
.
∴点![]() 的坐标为
的坐标为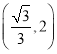 ;
;
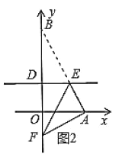
(ii)当![]() 时,如图2所示.
时,如图2所示.
∵![]() ,
,![]()
∴![]() ,
,
∴![]() .
.
在![]() 中,
中,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,![]() .
.
在![]() 中,
中,![]() ,
, ![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴点![]() 的坐标为
的坐标为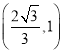 .
.
综上所述:当![]() 为直角三角形时,
为直角三角形时,![]() 点坐标为
点坐标为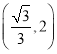 或
或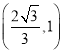 .
.
(II)由折叠可知:![]() ,
,
∴![]() ,
,![]() ,
,
又∵![]() ,
,
∴当点![]() 在
在![]() 轴上时,
轴上时,![]() 取最小值,如图3所示.
取最小值,如图3所示.
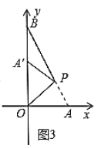
∵![]()
∴![]()
∴直线![]() 的解析式为
的解析式为![]()
设直线![]() 的解析式为
的解析式为![]() ,
,
将![]() 、
、![]() 代入
代入![]() 中,
中,
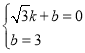 ,解得:
,解得: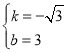 ,
,
∴直线![]() 的解忻式为
的解忻式为![]() .
.
联立直线![]() 、
、![]() 的解析式成方程组,
的解析式成方程组,
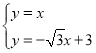 ,解得:
,解得: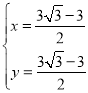 ,
,
∴.当![]() 取得最小值时,
取得最小值时,![]() 点坐标为
点坐标为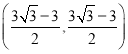 .
.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图在平面直角坐标系中,将△ABO绕点A顺时针旋转到△AB1C1的位置,点B、O分别落在点B1、C1处,点B1在x轴上,再将△AB1C1绕点B1顺时针旋转到△A1B1C2的位置,点C2在x轴上,将△A1B1C2绕点C2顺时针旋转到△A2B2C2的位置,点A2在x轴上,依次进行下去…若点A(![]() ,0),B(0,2),则点B2018的坐标为( )
,0),B(0,2),则点B2018的坐标为( )

A. (6048,0)B. (6054,0)C. (6048,2)D. (6054,2)
查看答案和解析>>
科目:初中数学 来源: 题型:
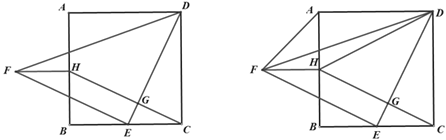
【题目】已知:在正方形ABCD中,点E在 BC边上,连接 DE,以DE为直角边作等腰直角三角形EDF(∠DEF=90°),过点C作 DE的垂线,垂足为G,交AB于点H,连接 FH.
(1)如图 1,求证:四边形FECH为平行四边形
(2)如图 2,连接 DH和 AF,点 E 为 BC 中点,在不添加任何辅助线与字母的情况下,请直接写出与平行四边形FECH面积相等的所有三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校开展课外活动,分音乐、体育、美术、制作四个活动项目,随机抽取部分学生对其选择参加的活动项目进行调查统计,制成了两幅不完整的统计图.
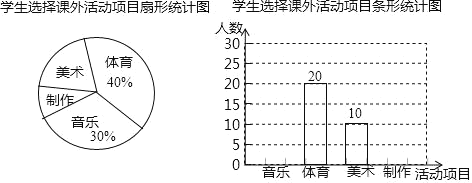
请根据上述统计图提供的信息,完成下列问题:
(1)这次抽查的样本容量是 ;
(2)请补全上述条形统计图,并求出扇形图中“美术”所占的圆心角度数;
(3)若该校有2000名学生,请你用此样本估计参加“艺术”类活动项目(“艺术”类活动包括“音乐”和“美术”两个项目)的学生人数约为多少人.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=-2,与x轴的一个交点在(-3,0)和(-4,0)之间,其部分图象如图所示.则下列结论:①4a-b=0;②c<0;③-3a+c>0;④4a-2b>at2+bt(t为实数);⑤点![]() ,
,![]() ,
,![]() 是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
是该抛物线上的点,则y1<y2<y3.其中正确结论的个数是( )
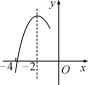
A.4B.3C.2D.1
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】将一个直角三角形纸片![]() ,放置在平面直角坐标系中,点
,放置在平面直角坐标系中,点![]() ,点
,点![]() ,点
,点![]()
(I)过边![]() 上的动点
上的动点![]() (点
(点![]() 不与点
不与点![]() ,
,![]() 重合)作
重合)作![]() 交
交![]() 于点
于点![]() ,沿着
,沿着![]() 折叠该纸片,点
折叠该纸片,点![]() 落在射线
落在射线![]() 上的点
上的点![]() 处.
处.
①如图,当![]() 为
为![]() 中点时,求
中点时,求![]() 点的坐标;
点的坐标;
②连接![]() ,当
,当![]() 为直角三角形时,求
为直角三角形时,求![]() 点坐标:
点坐标:
(Ⅱ)![]() 是
是![]() 边上的动点(点
边上的动点(点![]() 不与点
不与点![]() 重合),将
重合),将![]() 沿
沿![]() 所在的直线折叠,得到
所在的直线折叠,得到![]() ,连接
,连接![]() ,当
,当![]() 取得最小值时,求
取得最小值时,求![]() 点坐标(直接写出结果即可).
点坐标(直接写出结果即可).

查看答案和解析>>
科目:初中数学 来源: 题型:
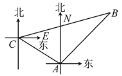
【题目】如图,甲、乙只捕捞船同时从A港出海捕鱼,甲船以每小时15![]() km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
km的速度沿北偏西60°方向前进,乙船以每小时15 km的速度沿东北方向前进.甲船航行2 h到达C处,此时甲船发现渔具丢在了乙船上,于是甲船快速(匀速)沿北偏东75°的方向追赶乙船,结果两船在B处相遇.问:
(1)甲船从C处出发追赶上乙船用了多少时间?
(2)甲船追赶乙船的速度是每小时多少千米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,抛物线y=![]() (x﹣m)2的顶点A在x轴正半轴上,交y轴于B点,S△OAB=1.
(x﹣m)2的顶点A在x轴正半轴上,交y轴于B点,S△OAB=1.

(1)求抛物线的解析式;
(2)如图2,P是第一象限内抛物线上对称轴右侧一点,过P的直线l与抛物线有且只有一个公共点,l交抛物线对称轴于C点,连PB交对称轴于D点,若∠BAO=∠PCD,求证:AC=2AD;
(3)如图3,以A为顶点作直角,直角边分别与抛物线交于M、N两点,当直角∠MAN绕A点旋转时,求证:MN始终经过一个定点,并求出该定点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于题目:在平面直角坐标系中,直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于
轴交于![]() 两点,过点
两点,过点![]() 且平行
且平行![]() 轴的直线与过点
轴的直线与过点![]() 且平行
且平行![]() 轴的直线相交于点
轴的直线相交于点![]() ,若抛物线
,若抛物线![]() 与线段
与线段![]() 有唯一公共点,求
有唯一公共点,求![]() 的取值范围.甲的计算结果是
的取值范围.甲的计算结果是![]() ;乙的计算结果是
;乙的计算结果是![]() ,则( )
,则( )
A.甲的结果正确B.乙的结果正确
C.甲与乙的结果合在一起正确D.甲与乙的结果合在一起也不正确
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com